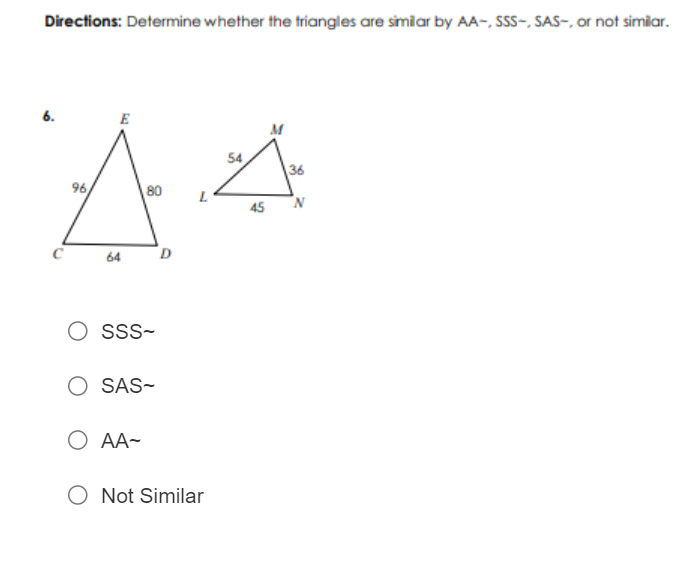
Determine whether the triangles are similar by AA~, SSS~, SAS~, or not similar.

Steps to Solve

1. Identify the sides of the triangles

For triangle ( CED ):

• Side ( CE = 96 )
• Side ( ED = 80 )
• Side ( CD = 64 )

For triangle ( LMN ):

• Side ( LM = 54 )
• Side ( MN = 36 )
• Side ( LN = 45 )

2. Determine the ratios of corresponding sides

Now let's find the ratios of corresponding sides:

• Ratio of ( CE ) to ( LM ): $$ \frac{CE}{LM} = \frac{96}{54} = \frac{16}{9} $$

• Ratio of ( ED ) to ( MN ): $$ \frac{ED}{MN} = \frac{80}{36} = \frac{20}{9} $$

• Ratio of ( CD ) to ( LN ): $$ \frac{CD}{LN} = \frac{64}{45} $$

3. Compare the ratios for similarity

To determine if the triangles are similar by SSS, all ratios must be equal. Compare the calculated ratios:

• ( \frac{CE}{LM} = \frac{16}{9} )
• ( \frac{ED}{MN} = \frac{20}{9} )
• ( \frac{CD}{LN} ) has different= values

Since ( \frac{96}{54} ) and ( \frac{80}{36} ) are not equal, the triangles are not similar by SSS.

4. Check angles if applicable (AA or SAS)

To determine similarity, we must check if any angles correspond. If we do not know angles, we cannot confirm AA or SAS.

Hence, using SSS shows they are not similar, and without angle information, we cannot confirm do AA or SAS.