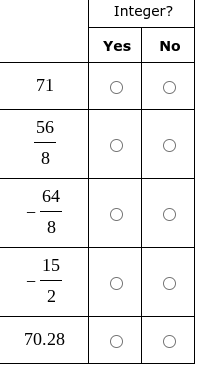
Determine whether each of the following numbers is an integer: 71, 56/8, 64/8, 15/2, 70.28.
Understand the Problem
The question is asking whether each of the given values, which include both whole numbers and fractions, are integers. To address this, we will evaluate each value by calculating the results of the fractions and then determining if each result is a whole number.
Answer
Yes for 71, $ \frac{56}{8} $, and $ -\frac{64}{8} $; No for $ -\frac{15}{2} $ and 70.28.
Answer for screen readers
- Yes for 71, $ \frac{56}{8} $, and $ -\frac{64}{8} $.
- No for $ -\frac{15}{2} $ and 70.28.
Steps to Solve
- Evaluate the Whole Number
The first value is 71. Since this is a whole number, we classify it as an integer.
- Calculate the Fraction
For the next value, we need to evaluate $ \frac{56}{8} $.
Calculating this gives:
$$ \frac{56}{8} = 7 $$
Since 7 is a whole number, it is an integer.
- Evaluate the Subtraction of the Fraction
Next, we evaluate $ -\frac{64}{8} $.
Calculating this gives:
$$ -\frac{64}{8} = -8 $$
Since -8 is a whole number, it is also an integer.
- Calculate Another Fraction
Now we calculate $ -\frac{15}{2} $.
Calculating this gives:
$$ -\frac{15}{2} = -7.5 $$
Since -7.5 is not a whole number, it is not an integer.
- Evaluate the Decimal
Finally, we examine 70.28. Since this is a decimal, it is not a whole number, so it is also not an integer.
- Yes for 71, $ \frac{56}{8} $, and $ -\frac{64}{8} $.
- No for $ -\frac{15}{2} $ and 70.28.
More Information
An integer is a whole number that can be positive, negative, or zero, but it cannot be a fraction or a decimal. In this case, 71, 7 ($ \frac{56}{8} $), and -8 ($ -\frac{64}{8} $) fit this definition, while -7.5 and 70.28 do not.
Tips
- Misinterpreting fractions and assuming they are integers without calculating them.
- Confusing decimals with integers; it’s important to recognize that decimals with non-zero figures after the point are not considered integers.