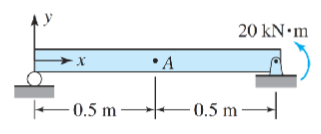
Determine the reactions at the supports A and B for the beam subjected to a moment of 20 kN·m.

Steps to Solve

1. Identify the Forces and Moments Acting on the Beam

The beam is subjected to a moment of $20 , \text{kN} \cdot \text{m}$ at the right end. We also have supports at points A (roller support) and B (fixed support).

2. Draw a Free Body Diagram (FBD)

Draw the FBD of the beam showing reactions at A and B. At point A, there will be a vertical reaction force $R_A$ and at point B, a vertical reaction force $R_B$ and a moment $M_B$.

3. Use Equilibrium Equations

Apply the equations of equilibrium:

• Sum of vertical forces ($\Sigma F_y = 0$): $$ R_A + R_B = 0 $$

• Sum of moments about point B ($\Sigma M_B = 0$): $$ -20 , \text{kN} \cdot \text{m} + R_A(1.0 , \text{m}) = 0 $$

4. Solve the Moment Equation for $R_A$

Rearranging the moment equation: $$ R_A(1.0 , \text{m}) = 20 , \text{kN} \cdot \text{m} $$ $$ R_A = \frac{20 , \text{kN} \cdot \text{m}}{1.0 , \text{m}} = 20 , \text{kN} $$

5. Substitute for $R_B$

Using the first equilibrium equation: $$ R_B = -R_A = -20 , \text{kN} $$

This means the beam has vertical reaction forces that add up to zero.