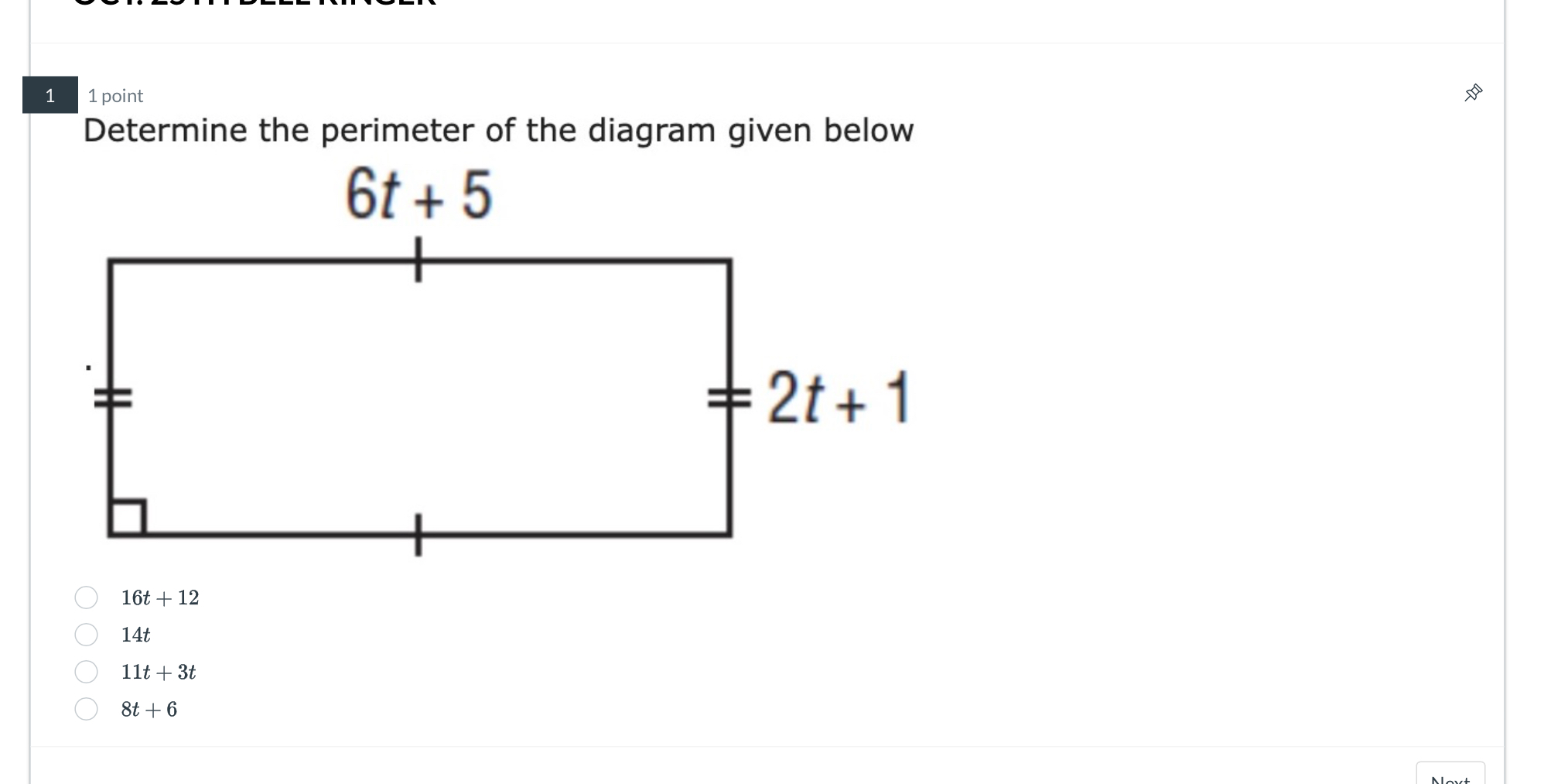
Determine the perimeter of the diagram given below.
Understand the Problem
The question is asking to determine the perimeter of a rectangle, given the lengths of its sides represented as algebraic expressions. We need to add together the expressions for the length and width to calculate the perimeter.
Answer
The perimeter is $16t + 12$.
Answer for screen readers
The perimeter of the rectangle is $16t + 12$.
Steps to Solve
-
Identify Lengths of Sides We have the expressions for the length and width of the rectangle. The length is given as $6t + 5$ and the width is $2t + 1$.
-
Formula for Perimeter The formula for the perimeter $P$ of a rectangle is given by: $$ P = 2(\text{Length} + \text{Width}) $$
-
Substitute in Length and Width Now substitute the length and width into the perimeter formula: $$ P = 2((6t + 5) + (2t + 1)) $$
-
Combine Like Terms Inside the parentheses, combine the like terms: $$ (6t + 5) + (2t + 1) = 6t + 2t + 5 + 1 = 8t + 6 $$
-
Calculate the Perimeter Now, multiply the expression by 2: $$ P = 2(8t + 6) = 16t + 12 $$
The perimeter of the rectangle is $16t + 12$.
More Information
The perimeter provides the total distance around the rectangle, factoring in the algebraic expressions for its sides. This is a common calculation in geometry, especially when variables are involved.
Tips
- Incorrectly adding the length and width: It's important to ensure like terms are combined properly.
- Forgetting to multiply by 2: Make sure to use the perimeter formula correctly after adding the sides.
