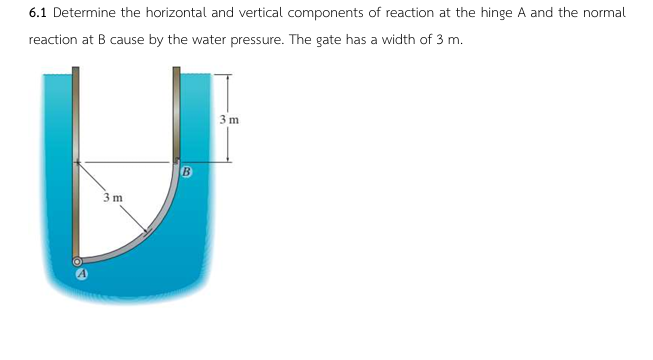
Determine the horizontal and vertical components of reaction at hinge A and the normal reaction at B caused by the water pressure. The gate has a width of 3 m.

Understand the Problem

The question is asking to determine the horizontal and vertical components of reaction forces at hinge A of the gate, as well as the normal reaction force at point B, due to water pressure acting on the gate. The given width of the gate is 3 meters, and there are dimensions indicating the vertical height of water. The approach will involve applying principles of fluid mechanics and static equilibrium.

Answer

The horizontal reaction at hinge A is $H = 264.3 \, kN$, the vertical reaction is $V = 38 \, kN$, and the normal reaction force at B is $N = 226.3 \, kN$.

Steps to Solve

Determine the Hydrostatic Pressure Force

The hydrostatic pressure force ($F_p$) can be calculated using the formula:

$$ F_p = \rho g h A $$

Where:

$\rho$ is the density of water (approximately $1000 , kg/m^3$)
$g$ is the acceleration due to gravity (approximately $9.81 , m/s^2$)
$h$ is the height of water (3 m in this case)
$A$ is the area of the gate submerged in water

In this case:

$$ A = \text{width} \times \text{height} = 3 , m \times 3 , m = 9 , m^2 $$

So the pressure force is:

$$ F_p = 1000 \times 9.81 \times 3 \times 9 = 264.3 , kN $$

Calculate the Center of Pressure

The center of pressure ($h_{cp}$) below the surface is given by:

$$ h_{cp} = \frac{I_G}{A \cdot \bar{y}} + \bar{y} $$

Where:

$\bar{y}$ is the depth to the centroid of the area (1.5 m for a 3 m high gate)
$I_G$ is the moment of inertia about the horizontal axis through the centroid, which for a rectangle is given by:

$$ I_G = \frac{b \cdot h^3}{12} $$

For our case with $b = 3 , m$ and $h = 3 , m$:

$$ I_G = \frac{3 \cdot 3^3}{12} = 6.75 , m^4 $$

Now calculate the center of pressure:

$$ h_{cp} = \frac{6.75}{9 \cdot 1.5} + 1.5 = 1.75 , m $$

Determine the Horizontal and Vertical Components of the Forces

The horizontal component of the force ($H$) at hinge A is equal to the hydrostatic force since there's no horizontal movement:

$$ H = F_p = 264.3 , kN $$

The vertical component ($V$) can be analyzed by the equilibrium of forces. The vertical reaction at hinge A and the normal force at B must balance the resultant force of the hydrostatics acting downwards:

$$ V + N = F_p $$

Compute the Normal Reaction Force at B

Calculate the moment about hinge A for equilibrium:

$$ N \cdot h_{cp} = F_p \cdot \bar{y} $$

Substituting the values:

$$ N \cdot 1.75 = 264.3 \cdot 1.5 $$

Thus,

$$ N = \frac{264.3 \cdot 1.5}{1.75} = 226.3 , kN $$

Finally substituting back to find the vertical force component:

$$ V = F_p - N = 264.3 - 226.3 = 38 , kN $$

The horizontal and vertical components of reaction at hinge A are $H = 264.3 , kN$ and $V = 38 , kN$, respectively. The normal reaction force at B is $N = 226.3 , kN$.

More Information

The calculations involved hydrostatic pressure, the center of pressure, and applying equilibrium conditions to find the forces acting on the gate submerged in water.

Tips

Failing to calculate the correct area for the hydrostatic force.
Forgetting to use the correct depth for centroid when calculating the center of pressure.
Not considering equilibrium conditions correctly.

Thank you for voting!