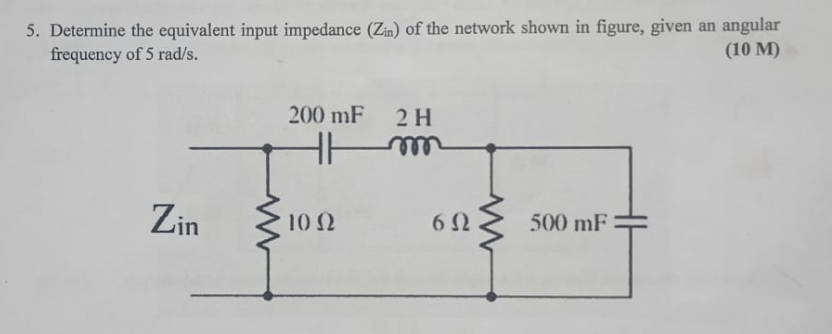
Determine the equivalent input impedance (Zin) of the network shown in figure, given an angular frequency of 5 rad/s.

Steps to Solve

1. Calculate the impedance of the capacitor (C1)

The impedance of a capacitor is given by the formula: $$ Z_C = \frac{1}{j \omega C} $$ Where:

• $\omega = 5 , \text{rad/s}$
• $C = 200 , \text{mF} = 0.2 , \text{F}$

Substituting the values: $$ Z_{C1} = \frac{1}{j \cdot 5 \cdot 0.2} = \frac{1}{j} = -j $$

2. Calculate the impedance of the inductor (L1)

The impedance of an inductor is given by the formula: $$ Z_L = j \omega L $$ Where:

• $L = 2 , \text{H}$

Substituting the values: $$ Z_{L1} = j \cdot 5 \cdot 2 = 10j $$

3. Calculate the impedance of the capacitor (C2)

Again using the capacitor impedance formula: $$ Z_{C2} = \frac{1}{j \omega C} $$ Where:

• $C = 500 , \text{mF} = 0.5 , \text{F}$

Substituting the values: $$ Z_{C2} = \frac{1}{j \cdot 5 \cdot 0.5} = \frac{1}{2.5j} = -\frac{j}{2.5} $$

4. Combine the impedances in series and parallel

The capacitor C1 is in series with the inductor L1: $$ Z_{series} = Z_{C1} + Z_{L1} = -j + 10j = 9j $$

Now, this series combination is in parallel with the resistance (10 Ω) and the impedance of C2: $$ Z_{\text{parallel}} = \frac{Z_{series} \cdot Z_{C2}}{Z_{series} + Z_{C2}} $$

5. Calculate the total impedance

Let’s first find $Z_{\text{parallel}}$ with C2 (assumed to be in parallel with the series combination):

1. Convert C2 impedance: $$ Z_{C2} = -\frac{j}{2.5} $$

2. Calculate the equivalent: Since the process involves complex numbers, use the formula to find the total impedance. Combine $Z_{parallel}$ with the 10 Ω resistance.

3. Total Input Impedance (Zin)

Now, combine everything to determine the total input impedance $Z_{in}$: Combine the total parallel impedance with the additional resistances.