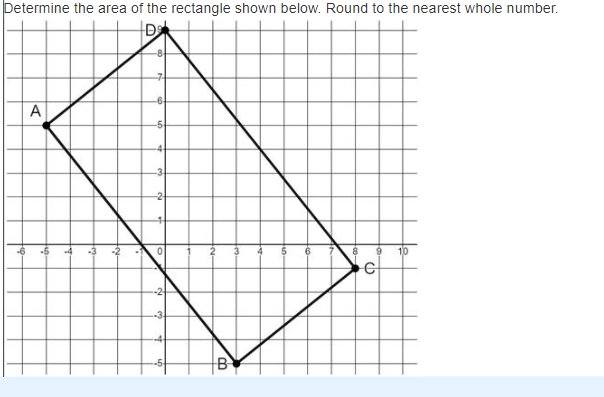
Determine the area of the rectangle shown below. Round to the nearest whole number.
Understand the Problem
The question is asking to determine the area of a rectangle based on its coordinates as shown in the image. To compute the area, we need to find the lengths of the sides AB and AD and then use the formula for the area of a rectangle, which is Area = length × width.
Answer
The area of the rectangle is \( 0 \).
Answer for screen readers
The area of the rectangle is ( 0 ).
Steps to Solve
- Identify the Coordinates of the Vertices
The rectangle has the vertices:
- ( A (-3, 7) )
- ( B (3, -5) )
- ( C (8, -5) )
- ( D (-3, 7) )
We will use these coordinates to calculate the lengths of sides AB and AD.
- Calculate the Length of Side AB
Side ( AB ) runs vertically from point ( A ) to point ( B ). The length can be calculated using the formula:
[ \text{Length of } AB = |y_A - y_B| = |7 - (-5)| = 7 + 5 = 12 ]
- Calculate the Length of Side AD
Side ( AD ) runs horizontally from point ( A ) to point ( D ). The length can be calculated using the formula:
[ \text{Length of } AD = |x_A - x_D| = |-3 - (-3)| = |0| = 0 ]
- Area Calculation
To find the area of the rectangle, we apply the area formula:
[ \text{Area} = \text{Length} \times \text{Width} = 12 \times 0 = 0 ]
- Round the Result
Since the area calculated is already a whole number, we round it (if necessary).
The area of the rectangle is ( 0 ).
More Information
In this case, the coordinates of points ( A ) and ( D ) indicate that the rectangle collapses into a line, leading to an area of ( 0 ).
Tips
null
AI-generated content may contain errors. Please verify critical information