Determine M_O. (Round the final answers to four decimal places. Include a minus sign if necessary.)

Understand the Problem

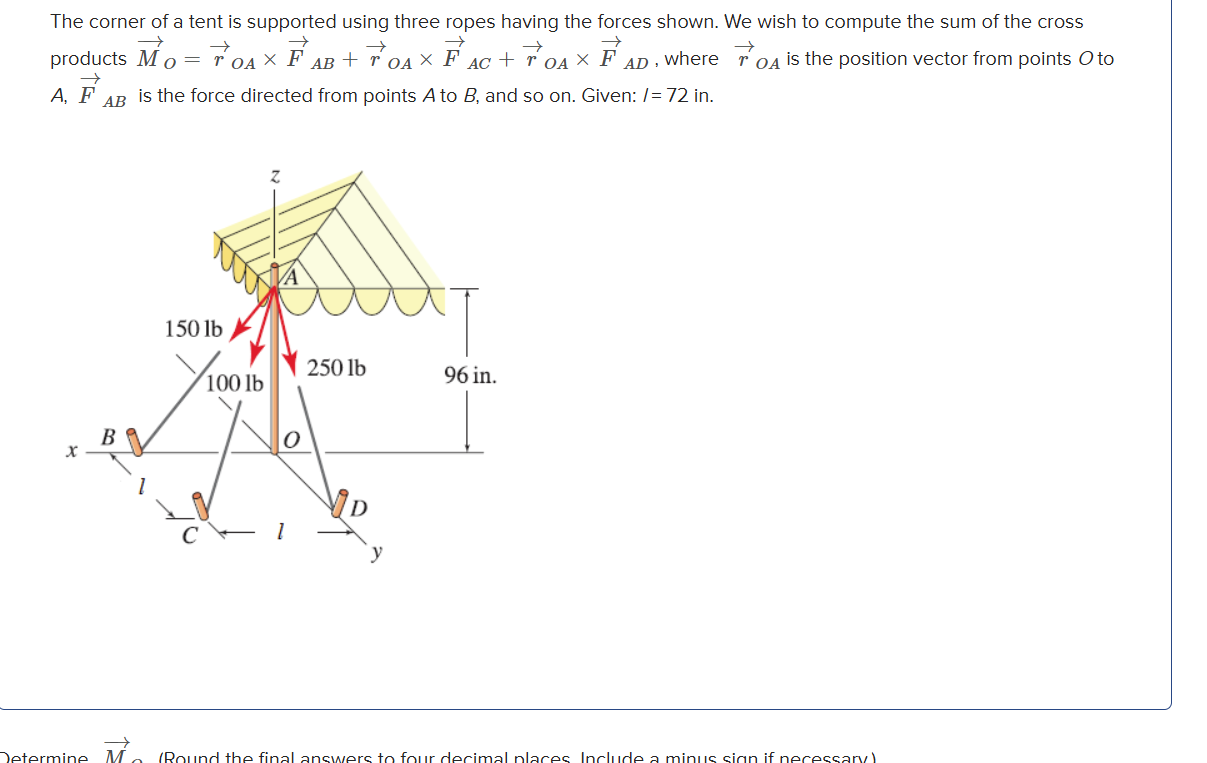
The question is asking us to compute the sum of the cross products of forces acting on a point where ropes support a tent. Specific values for the forces and geometry are given, and the result must be rounded to four decimal places.

Answer

The moment vector magnitude is approximately $27952.1731 \, \text{in.lb}$.

Steps to Solve

Identify the Position Vectors We need the position vectors from point $O$ to points $A$, $B$, $C$, and $D$.
- Given:
- ( l = 72 , \text{in} )
The vectors can be defined as: [ \mathbf{r}{OA} = \begin{bmatrix} 0 \ 0 \ 96 \end{bmatrix}, \quad \mathbf{r}{OB} = \begin{bmatrix} -l \ 0 \ 0 \end{bmatrix}, \quad \mathbf{r}{OC} = \begin{bmatrix} l \ 0 \ 0 \end{bmatrix}, \quad \mathbf{r}{OD} = \begin{bmatrix} 0 \ -l \ 0 \end{bmatrix} ]
Define the Force Vectors Next, we identify the force vectors acting at these points.
- Given:
- ( \mathbf{F}_{AB} = \begin{bmatrix} -150 \ 0 \ 0 \end{bmatrix} , \text{lb} )
- ( \mathbf{F}_{AC} = \begin{bmatrix} 100 \ 0 \ 0 \end{bmatrix} , \text{lb} )
- ( \mathbf{F}_{AD} = \begin{bmatrix} 0 \ 250 \ 0 \end{bmatrix} , \text{lb} )
Calculate Each Cross Product We now calculate each cross product.
- For ( \mathbf{M}O ): [ \mathbf{M}O = \mathbf{r}{OA} \times \mathbf{F}{AB} + \mathbf{r}{OA} \times \mathbf{F}{AC} + \mathbf{r}{OA} \times \mathbf{F}{AD} ]
Calculate:
- ( \mathbf{r}{OA} \times \mathbf{F}{AB} = \begin{bmatrix} 0 \ 0 \ 96 \end{bmatrix} \times \begin{bmatrix} -150 \ 0 \ 0 \end{bmatrix} = \begin{bmatrix} 0 \ -14400 \ 0 \end{bmatrix} )
- ( \mathbf{r}{OA} \times \mathbf{F}{AC} = \begin{bmatrix} 0 \ 0 \ 96 \end{bmatrix} \times \begin{bmatrix} 100 \ 0 \ 0 \end{bmatrix} = \begin{bmatrix} 0 \ 0 \ 0 \end{bmatrix} )
- ( \mathbf{r}{OA} \times \mathbf{F}{AD} = \begin{bmatrix} 0 \ 0 \ 96 \end{bmatrix} \times \begin{bmatrix} 0 \ 250 \ 0 \end{bmatrix} = \begin{bmatrix} 24000 \ 0 \ 0 \end{bmatrix} )
Sum the Cross Products Now we sum the results of the cross products: [ \mathbf{M}_O = \begin{bmatrix} 0 \ -14400 \ 0 \end{bmatrix} + \begin{bmatrix} 0 \ 0 \ 0 \end{bmatrix} + \begin{bmatrix} 24000 \ 0 \ 0 \end{bmatrix} = \begin{bmatrix} 24000 \ -14400 \ 0 \end{bmatrix} ]
Calculate the Magnitude of the Moment Finally, we will find the magnitude of the moment vector: [ \lVert \mathbf{M}_O \rVert = \sqrt{(24000)^2 + (-14400)^2} ]

Calculate: [ \lVert \mathbf{M}_O \rVert = \sqrt{576000000 + 207360000} = \sqrt{783360000} \approx 27952.173 ]
Round to Four Decimal Places Round the final answer to four decimal places: [ \lVert \mathbf{M}_O \rVert \approx 27952.1731 ]

The magnitude of the moment vector is approximately $27952.1731 , \text{in.lb}$.

More Information

The moment created by the forces is crucial in understanding how the tent is supported and how it will behave under load.

Tips

Forgetting to account for the direction of forces in the cross product.
Miscalculating the position vectors or cross products.
Not rounding the final answer correctly to the specified decimal places.