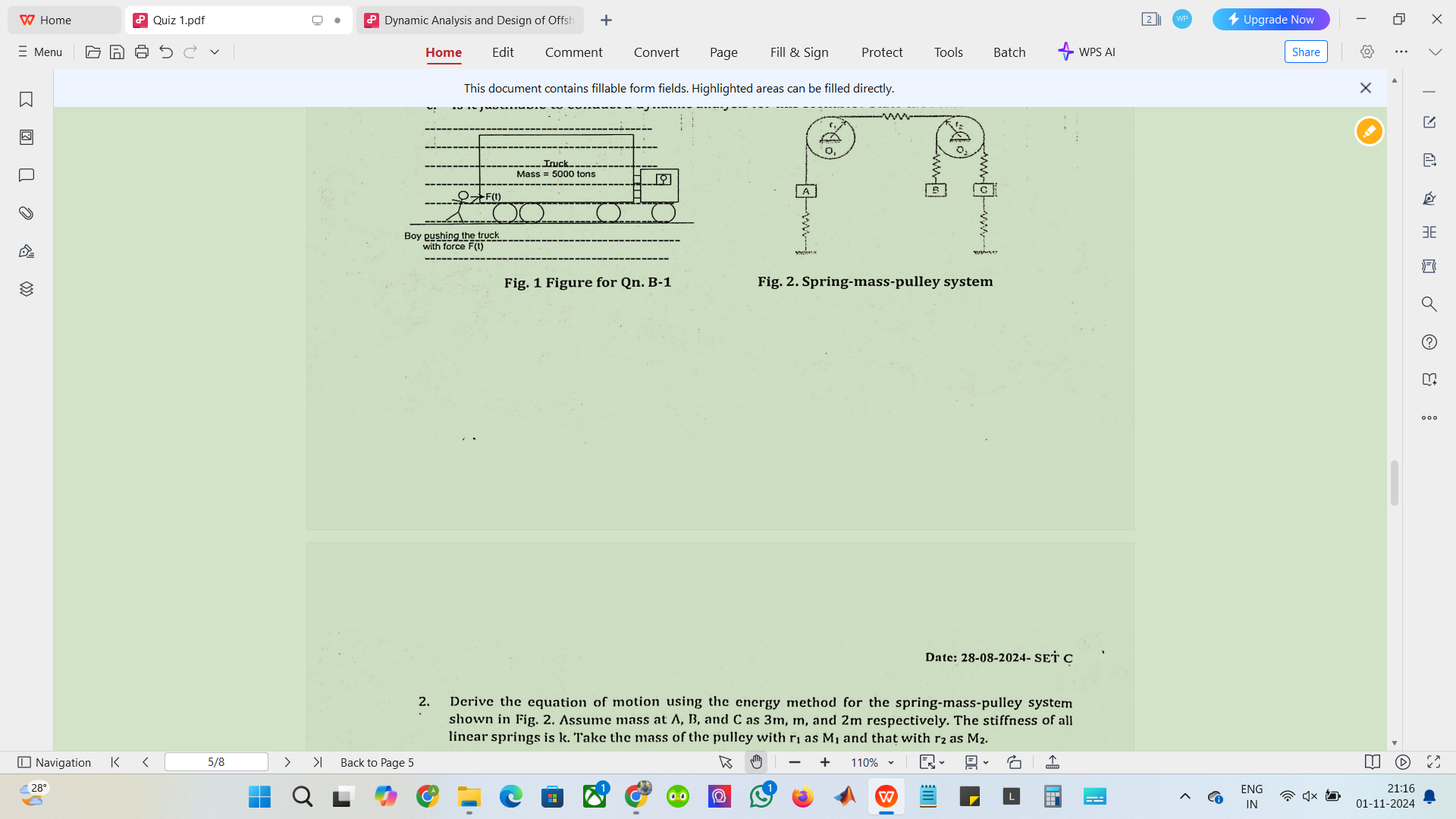
Derive the equation of motion using the energy method for the spring-mass-pulley system shown in the figure. Assume mass at A, B, and C as 3m, m, and 2m respectively. The stiffness... Derive the equation of motion using the energy method for the spring-mass-pulley system shown in the figure. Assume mass at A, B, and C as 3m, m, and 2m respectively. The stiffness of all linear springs is k. Take the mass of the pulley with r1 as M1 and that with r2 as M2.
Understand the Problem
The question is asking to derive the equation of motion for a spring-mass-pulley system using the energy method, considering given parameters and properties of masses and springs.
Answer
The equation of motion is given by $m\frac{d^2x}{dt^2} + kx = 0$.
Answer for screen readers
The equation of motion for the spring-mass-pulley system can be expressed in a form derived from energy conservation, typically represented as:
$$ m\frac{d^2x}{dt^2} + kx = 0 $$
where ( x ) is the displacement of the mass from its equilibrium position.
Steps to Solve
- Identify the System Energies
The total mechanical energy of the system consists of the gravitational potential energy (GPE) and the elastic potential energy (EPE) of the springs.
- Gravitational Potential Energy
The gravitational potential energy for each mass is given by:
For mass at A (3m):
$$ GPE_A = 3mgh_A $$
For mass at B (m):
$$ GPE_B = mgh_B $$
For mass at C (2m):
$$ GPE_C = 2mgh_C $$
Where ( h_A, h_B, ) and ( h_C ) are the respective heights of A, B, and C from a reference point.
- Elastic Potential Energy
The elastic potential energy stored in a spring is given by:
$$ EPE = \frac{1}{2} k x^2 $$
where ( k ) is the spring constant and ( x ) is the displacement from the equilibrium position.
- Total Energy of the System
The total mechanical energy ( E ) of the system is given by the sum of the gravitational potential energies and elastic potential energies:
$$ E = GPE_A + GPE_B + GPE_C + \sum EPE $$
- Use the Energy Conservation Principle
According to the principle of conservation of energy, the total mechanical energy remains constant if there are no non-conservative forces acting on it. Thus,
$$ E_{\text{initial}} = E_{\text{final}} $$
- Differentiate to Find Equation of Motion
To derive the equations of motion, differentiate the expression for total energy with respect to time:
$$ \frac{dE}{dt} = 0 $$
This will yield the equations of motion for the system.
- Set Up the Differential Equation
Express the heights ( h_A, h_B, h_C ) in terms of the displacements of the masses and set up the differential equation based on the terms derived from energy conservation.
The equation of motion for the spring-mass-pulley system can be expressed in a form derived from energy conservation, typically represented as:
$$ m\frac{d^2x}{dt^2} + kx = 0 $$
where ( x ) is the displacement of the mass from its equilibrium position.
More Information
The derivation of the equation of motion for systems involving springs and masses is often examined in dynamics and engineering mechanics as it demonstrates fundamental principles of energy conservation. Different configurations may yield different forms of the equation.
Tips
- Forgetting to include all potential energies: Ensure that gravitational and elastic potential energies are accounted for.
- Incorrectly setting up the reference height: Choose a consistent reference for measuring heights of masses.
- Neglecting mass effects on acceleration: Remember to apply Newton's second law correctly when deriving motion equations.
AI-generated content may contain errors. Please verify critical information