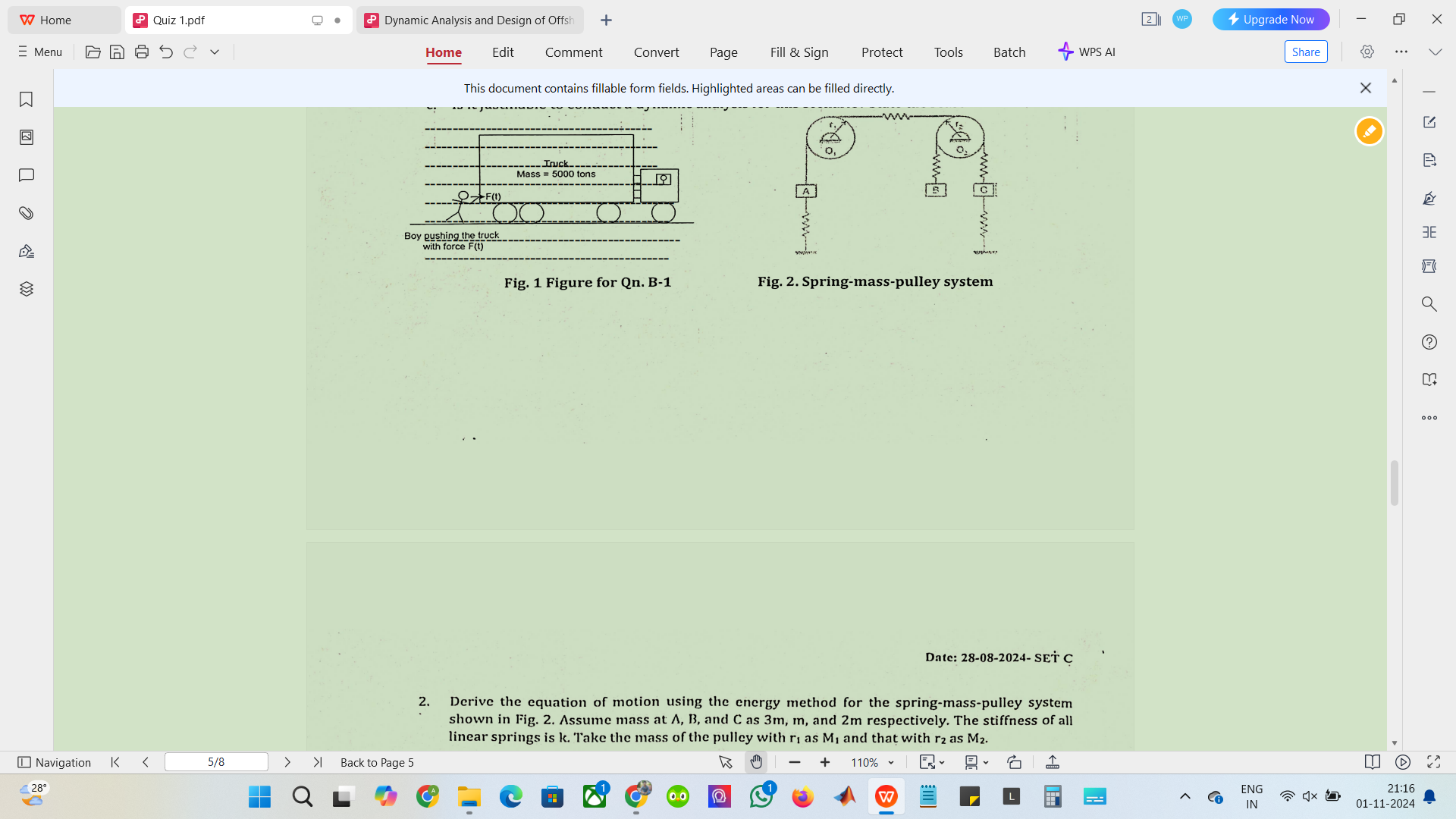
Derive the equation of motion and give me the free body diagram of the spring-pulley system.

Steps to Solve

1. Identify the components of the system
   The spring-mass-pulley system consists of three mass points (m, m, and m) connected by springs. The spring constants are $k_1$ and $k_2$ for the springs connected to masses A and C, respectively.

2. Define energy in the system
   The total energy in the system includes both potential energy stored in the springs and the kinetic energy of the masses:
   $$ E = PE_s + KE $$
   Where:

• $PE_s$ is the potential energy in the springs:
  $$ PE_s = \frac{1}{2}k_1 x_1^2 + \frac{1}{2}k_2 x_2^2 $$
• $KE$ is the total kinetic energy of the masses:
  $$ KE = \frac{1}{2}m_1 v_1^2 + \frac{1}{2}m_2 v_2^2 + \frac{1}{2}m_3 v_3^2 $$

3. Apply the work-energy principle
   According to the work-energy principle, the work done by the forces on the system equals the change in total energy:
   $$ W = \Delta E $$
   The work done due to the displacement of the masses and stretching of the springs must be calculated.

4. Set up the equations
   From the forces acting on each mass, set up the equations of motion using Newton's second law for each mass:

• For masses A and B:
  $$ m \frac{d^2x_1}{dt^2} = -k_1 x_1 + k_2 (x_2 - x_1) $$
• For mass C:
  $$ m \frac{d^2x_2}{dt^2} = -k_2 (x_2 - x_1) $$

5. Combine and simplify equations
   By substituting the equations of motion and combining them, you can derive a single second-order differential equation that describes the motion of one of the masses in the system.

6. Solve the differential equations
   This involves finding the characteristic equation and solving for the amplitudes and angular frequencies of the system to get the general solution.

7. Draw the Free Body Diagram (FBD)
   For the Free Body Diagram (FBD): Label all forces acting on each mass, including spring forces and gravitational forces.