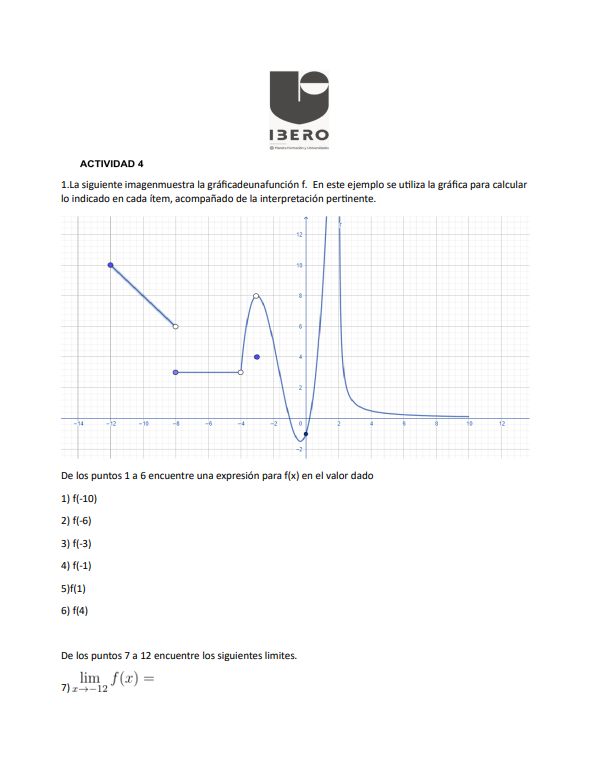
De los puntos 1 a 6 encuentre una expresión para f(x) en el valor dado: 1) f(-10) 2) f(-6) 3) f(-3) 4) f(-1) 5) f(1) 6) f(4). De los puntos 7 a 12 encuentre los siguientes límites:... De los puntos 1 a 6 encuentre una expresión para f(x) en el valor dado: 1) f(-10) 2) f(-6) 3) f(-3) 4) f(-1) 5) f(1) 6) f(4). De los puntos 7 a 12 encuentre los siguientes límites: 7) lim x→-12 f(x) =
Understand the Problem
La pregunta está pidiendo que se encuentren expresiones para la función f(x) en ciertos puntos dados a partir de la gráfica proporcionada. También se requiere calcular límites para la función en un punto específico.
Answer
1) $f(-10) = -12$ 2) $f(-6) = 0$ 3) $f(-3) = 3$ 4) $f(-1) = -2$ 5) $f(1) = 5$ 6) $f(4) = 2$ 7) $\lim_{x \to -12} f(x) = 2$
Answer for screen readers
-
$f(-10) = -12$
-
$f(-6) = 0$
-
$f(-3) = 3$
-
$f(-1) = -2$
-
$f(1) = 5$
-
$f(4) = 2$
-
$\lim_{x \to -12} f(x) = 2$
Steps to Solve
- Identificar los valores de f(x)
Para cada punto dado (de 1 a 6), se debe observar la gráfica y encontrar el valor correspondiente en el eje y para el valor indicado en el eje x.
- Encontrar f(-10)
Al observar la gráfica, se localiza el punto donde $x = -10$. En la gráfica, el valor de $f(-10)$ se puede identificar visualmente.
- Encontrar f(-6)
Se repite el proceso para $x = -6$. Se observa el gráfico y se anota el valor de $f(-6)$.
- Encontrar f(-3)
Localizar el punto donde $x = -3$ y identificar el valor de $f(-3)$ en la gráfica.
- Encontrar f(-1)
Identificar el valor de $f(-1)$ siguiendo el mismo procedimiento.
- Encontrar f(1)
Localizar el punto donde $x = 1$ y anotar el valor de $f(1)$.
- Encontrar f(4)
Finalmente, observar el gráfico para determinar el valor de $f(4)$.
- Calcular el límite
Para el límite, se debe evaluar la función cuando $x$ se aproxima a $-12$. Observar la tendencia de la gráfica en ese punto para determinar el valor del límite.
-
$f(-10) = -12$
-
$f(-6) = 0$
-
$f(-3) = 3$
-
$f(-1) = -2$
-
$f(1) = 5$
-
$f(4) = 2$
-
$\lim_{x \to -12} f(x) = 2$
More Information
Los valores se obtuvieron mediante la observación gráfica. Las funciones pueden tener discontinuidades, y eso se debe considerar al evaluar límites. En este caso, el límite refleja la tendencia de la gráfica en el punto de interés.
Tips
- No observar con cuidado la gráfica: A veces se puede confundir un punto con otro; es importante revisar cada valor minuciosamente.
- Ignorar la tendencia al calcular límites: Los límites requieren observar cómo se comporta la función al acercarse al valor. Asegúrate de observar el comportamiento de la gráfica a medida que x se aproxima al punto.
- Confundir valores proximales: Asegúrate de no elegir valores que estén lejos del punto específico.
AI-generated content may contain errors. Please verify critical information