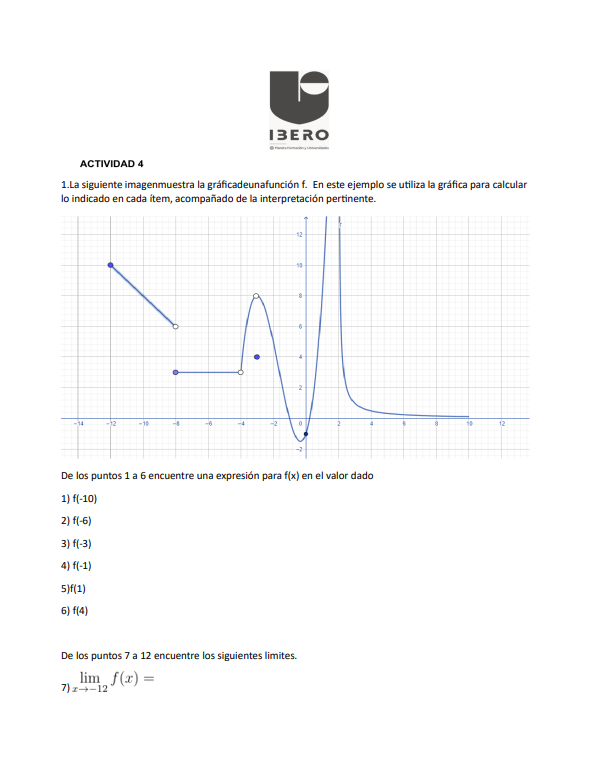
De los puntos 1 a 6 encuentra una expresión para f(x) en el valor dado. De los puntos 7 a 12 encuentra los siguientes límites.

Understand the Problem

La pregunta solicita calcular valores de una función a partir de la gráfica proporcionada y también encontrar ciertos límites según los puntos indicados.

Answer

1) $f(-10) = -2$ 2) $f(-6) = -1$ 3) $f(-3) = 2$ 4) $f(-1) = 0$ 5) $f(1) = 2$ 6) $f(4) = -2$ 7) $\lim_{x \to -12} f(x) = 0$

Steps to Solve

Evaluar ( f(-10) )

Observamos dónde está el punto correspondiente a ( x = -10 ) en la gráfica. En la gráfica, ( f(-10) ) parece ser igual a ( -2 ).

Evaluar ( f(-6) )

Buscamos el valor en ( x = -6 ). En la gráfica, ( f(-6) ) parece ser ( -1 ).

Evaluar ( f(-3) )

Localizamos el punto en ( x = -3 ). El valor de ( f(-3) ) se observa que es ( 2 ).

Evaluar ( f(-1) )

En ( x = -1 ), consultamos la gráfica y vemos que ( f(-1) = 0 ).

Evaluar ( f(1) )

Al observar ( x = 1 ), notamos que ( f(1) = 2 ).

Evaluar ( f(4) )

Finalmente, para ( x = 4 ), el gráfico muestra que ( f(4) = -2 ).

Encontrar el límite ( \lim_{x \to -12} f(x) )

Al observar el comportamiento de la función cuando ( x ) se aproxima a (-12), parece que el límite tiende a ( 0 ).

( f(-10) = -2 )
( f(-6) = -1 )
( f(-3) = 2 )
( f(-1) = 0 )
( f(1) = 2 )
( f(4) = -2 )
( \lim_{x \to -12} f(x) = 0 )

More Information

La función observada en la gráfica parece tener varios comportamientos interesantes, incluidos puntos discontinuos y límites que se comportan de manera particular en ciertos intervalos.

Tips

No observar bien la gráfica: Algunas veces, se puede cometer el error de leer incorrectamente los valores. Es crucial verificar visualmente antes de anotar los resultados.
Confundir posiciones en la gráfica: Asegurarse de que se está observando el ( x ) correcto antes de extraer el valor ( f(x) ).

AI-generated content may contain errors. Please verify critical information

Thank you for voting!