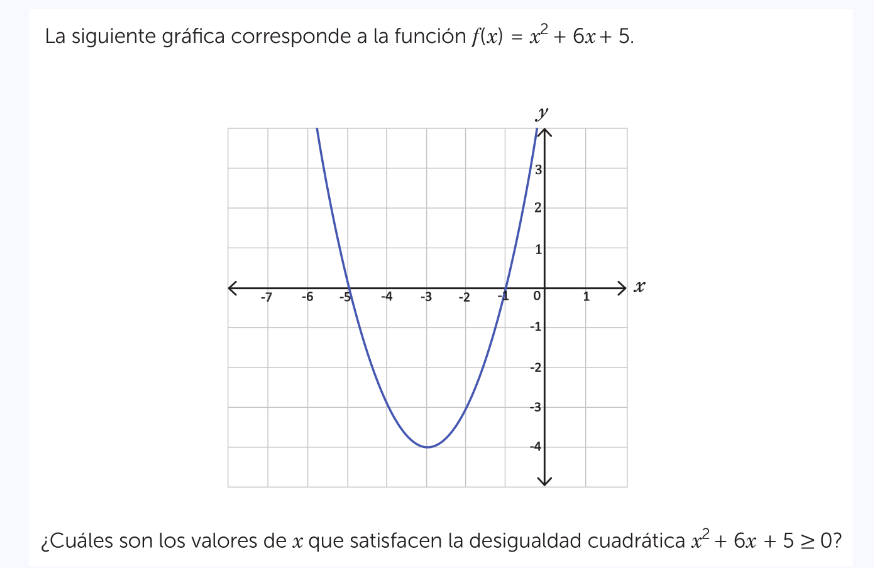
¿Cuáles son los valores de x que satisfacen la desigualdad cuadrática x² + 6x + 5 ≥ 0?

Steps to Solve

1. Encontrar las raíces de la ecuación cuadrática

Primero, resolvemos la ecuación cuadrática correspondiente, es decir, $x^2 + 6x + 5 = 0$. Usamos la fórmula cuadrática:

$$ x = \frac{{-b \pm \sqrt{{b^2 - 4ac}}}}{2a} $$

donde $a = 1$, $b = 6$, y $c = 5$.

2. Calcular el discriminante

Calculamos el discriminante:

$$ D = b^2 - 4ac = 6^2 - 4(1)(5) = 36 - 20 = 16 $$

Ya que $D > 0$, hay dos soluciones reales.

3. Obtener las raíces

Sustituyendo en la fórmula cuadrática:

$$ x = \frac{{-6 \pm \sqrt{16}}}{2(1)} $$

Calculamos las dos raíces:

$$ x_1 = \frac{{-6 + 4}}{2} = -1 $$

$$ x_2 = \frac{{-6 - 4}}{2} = -5 $$

4. Determinar intervalos y probar puntos

Los puntos donde la parábola cruza el eje $x$ son $x = -1$ y $x = -5$. Los intervalos a investigar son:

• $(-\infty, -5)$
• $(-5, -1)$
• $(-1, \infty)$

Elegimos un valor de prueba en cada intervalo para ver dónde $x^2 + 6x + 5 \geq 0$.

5. Evaluar los intervalos

• Para $x = -6$ en $(-\infty, -5)$: $$ f(-6) = (-6)^2 + 6(-6) + 5 = 36 - 36 + 5 = 5 \geq 0 $$ (verdadero)

• Para $x = -3$ en $(-5, -1)$: $$ f(-3) = (-3)^2 + 6(-3) + 5 = 9 - 18 + 5 = -4 < 0 $$ (falso)

• Para $x = 0$ en $(-1, \infty)$: $$ f(0) = 0^2 + 6(0) + 5 = 5 \geq 0 $$ (verdadero)

Finalmente, también incluimos los puntos donde la parábola toca el eje $x$.

6. Conclusión sobre la desigualdad

Los valores de $x$ que satisfacen la desigualdad $x² + 6x + 5 ≥ 0$ son los intervalos $(-\infty, -5] \cup [-1, \infty)$.