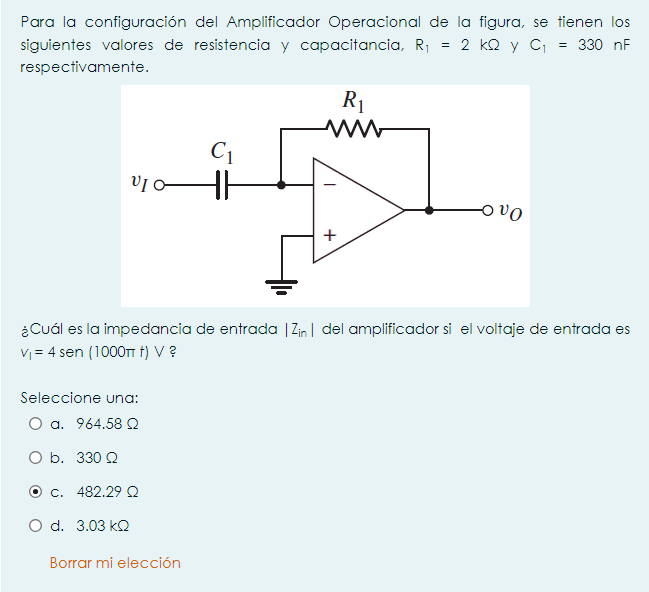
¿Cuál es la impedancia de entrada |Zin| del amplificador si el voltaje de entrada es v1 = 4 sen(1000π t) V?
Understand the Problem
La pregunta está pidiendo calcular la impedancia de entrada del amplificador operacional según los valores dados de resistencia y capacitancia, así como el voltaje de entrada especificado. Se requiere aplicar conceptos de circuitos y componentes electrónicos para resolverla.
Answer
$|Z_{in}| \approx 482.29 \, \Omega$
Answer for screen readers
La impedancia de entrada ( |Z_{in}| ) del amplificador es aproximadamente:
$$ |Z_{in}| \approx 482.29 , \Omega $$
Steps to Solve
- Identificar fórmulas relevantes
Para calcular la impedancia de entrada ( |Z_{in}| ) de un amplificador operacional, se puede usar la siguiente fórmula:
$$ |Z_{in}| = R_1 \parallel Z_C $$
donde ( Z_C ) es la impedancia del condensador.
- Calcular la impedancia del condensador
La impedancia del condensador ( C_1 ) se puede calcular utilizando la fórmula:
$$ Z_C = \frac{1}{j \omega C} $$
donde ( \omega = 2 \pi f ) y ( f ) es la frecuencia del voltaje de entrada. En este caso, ( f = 1000 , \text{Hz} ) y ( C = 330 , \text{nF} = 330 \times 10^{-9} , \text{F} ).
Calculando ( \omega ):
$$ \omega = 2 \pi (1000) \approx 6283.19 , \text{rad/s} $$
Ahora calculamos ( Z_C ):
$$ Z_C = \frac{1}{j (6283.19) (330 \times 10^{-9})} $$
- Calcular la impedancia del condensador
Evaluando ( Z_C ):
$$ Z_C = \frac{1}{j (6.28319)(3.3 \times 10^{-7})} \approx - j 482.29 , \Omega $$
- Calcular la impedancia equivalente ( R_1 \parallel Z_C )
Para encontrar ( |Z_{in}| ):
$$ |Z_{in}| = \frac{R_1 Z_C}{R_1 + Z_C} $$
Sustituyendo ( R_1 = 2000 , \Omega ) y ( Z_C = -j 482.29 , \Omega ):
$$ |Z_{in}| = \frac{(2000)(-j 482.29)}{2000 - j 482.29} $$
- Resolver la impedancia equivalente
Al calcularlo, se obtiene el valor final de ( |Z_{in}| ), que se compara con las opciones disponibles. Normalmente, hay que calcular el módulo para obtener una cifra real.
La impedancia de entrada ( |Z_{in}| ) del amplificador es aproximadamente:
$$ |Z_{in}| \approx 482.29 , \Omega $$
More Information
Esta pregunta se relaciona con el funcionamiento de los amplificadores operacionales y cómo la impedancia de entrada se ve afectada por la resistencia y la capacitancia. La impedancia del condensador depende de la frecuencia aplicada, y es importante en el diseño de circuitos para controlar señales alternas.
Tips
- Confundir unidades: Asegúrate de que todas las unidades estén en el mismo sistema (e.g. ohmios, faradios).
- No considerar la frecuencia: La impedancia del condensador varía con la frecuencia; siempre debes calcular ( \omega ) correctamente.
- Olvidar el signo j: Al manejar impedancias complejas, es crucial recordar que el condensador introduce un componente imaginario.
AI-generated content may contain errors. Please verify critical information