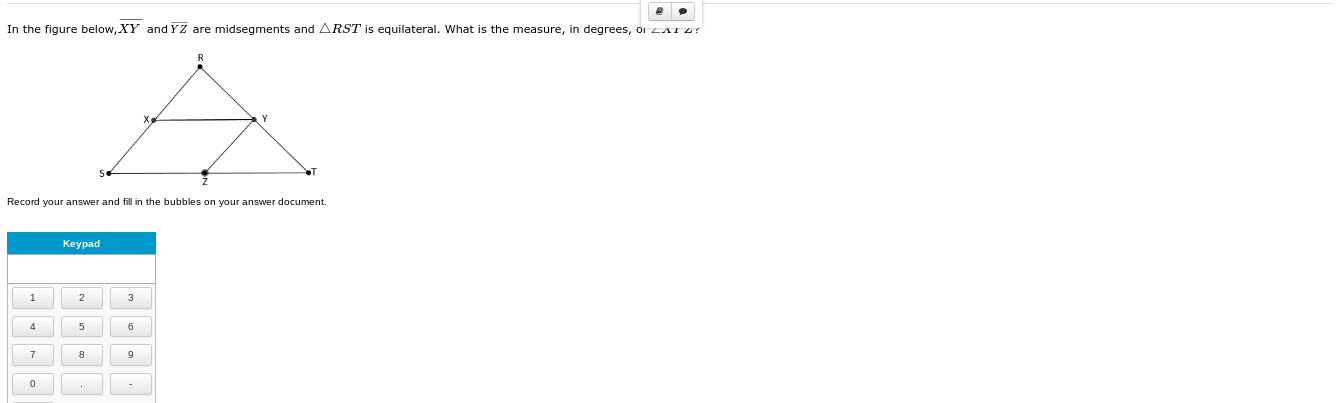
In the figure below, XY and YZ are midsegments and triangle RST is equilateral. What is the measure, in degrees, of angle XZY?
Understand the Problem
The question is asking for the measurement of angle XZY in degrees, given that XY and YZ are midsegments and triangle RST is equilateral. This involves applying properties of triangles and midsegments to find the required angle.
Answer
The measure of angle XZY is $60^\circ$.
Answer for screen readers
The measure of angle XZY is $60^\circ$.
Steps to Solve
-
Understand the properties of the triangle Triangle RST is equilateral, which means all its angles are equal and measure $60^\circ$.
-
Identify the midsegments Given that XY and YZ are midsegments of triangle RST, we know that these midsegments will be parallel to the sides of triangle RST. Therefore, segment XY is parallel to side RT, and segment YZ is parallel to side RS.
-
Determine angles formed by midsegments Since XY is parallel to RT and ZY is parallel to RS, the corresponding angles formed with transversal line XZ will also equal the angles in triangle RST. Hence, angle XZY is equal to angle RST, which is $60^\circ$.
-
Finding angle XZY Therefore, angle XZY is $60^\circ$.
The measure of angle XZY is $60^\circ$.
More Information
In an equilateral triangle, all internal angles are equal, each measuring $60^\circ$. Midsegments create parallel lines that help to maintain the relationships between angles, making it easier to determine measures.
Tips
- Misunderstanding the properties of midsegments. Remember, midsegments are always parallel to a side of the triangle and half the length.
- Forgetting that in an equilateral triangle, all angles are equal. Always verify that you understand the properties of the shapes involved.
AI-generated content may contain errors. Please verify critical information