cos 2x + 1 / sin 2x = cot x
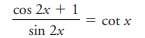
Understand the Problem
The question is asking to solve the trigonometric equation given in the image, which involves manipulating and simplifying trigonometric identities to find the values of x that satisfy the equation.
Answer
The solution holds true for any $x$ where both sides are defined, except where $\sin x = 0$.
Answer for screen readers
The solution to the equation is that it holds true for any $x$ where both sides are defined, except where $\sin x = 0$.
Steps to Solve
- Rewrite cotangent in terms of sine and cosine
Recall that the cotangent function can be expressed as: $$ \cot x = \frac{\cos x}{\sin x} $$
- Cross-multiply
Rearranging the equation gives: $$ \cos 2x + 1 = \cot x \cdot \sin 2x $$
So we can rewrite it as: $$ \cos 2x + 1 = \frac{\cos x}{\sin x} \cdot \sin 2x $$
- Substitute using the double angle identity for sine
Using the identity $\sin 2x = 2 \sin x \cos x$: $$ \cos 2x + 1 = \frac{\cos x}{\sin x} \cdot 2 \sin x \cos x $$
This simplifies to: $$ \cos 2x + 1 = 2 \cos^2 x $$
- Use the double angle identity for cosine
Recall that $\cos 2x = 2 \cos^2 x - 1$. Substitute this into the equation: $$ 2 \cos^2 x - 1 + 1 = 2 \cos^2 x $$
This simplifies to: $$ 2 \cos^2 x = 2 \cos^2 x $$
- Conclude
Since we have demonstrated an identity, it means the original equation holds for any $x$ where both sides are defined.
The solution to the equation is that it holds true for any $x$ where both sides are defined, except where $\sin x = 0$.
More Information
This equation leverages trigonometric identities and properties, demonstrating that some equations can hold universally under certain conditions, specifically those that don’t cause division by zero.
Tips
- Forgetting to consider the restrictions on $x$ where $\sin x = 0$, which leads to undefined cotangent.
- Misapplying trigonometric identities can lead to incorrect conclusions.
AI-generated content may contain errors. Please verify critical information