Convert from standard form to vertex form: y = x^2 + 8x + 11
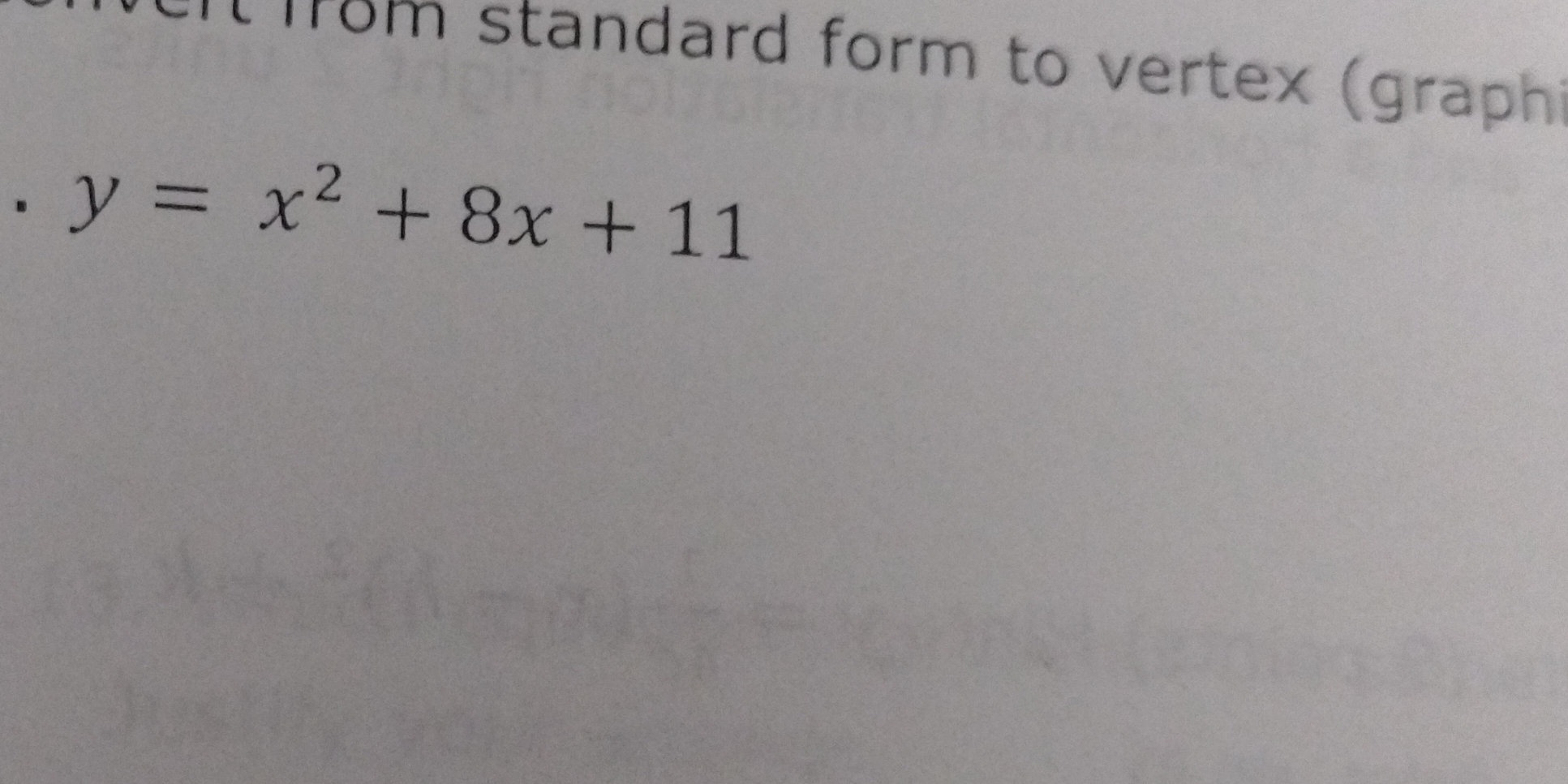
Understand the Problem
The question is asking to convert the quadratic equation from standard form to vertex form. The equation provided is in standard form and requires completing the square to find its vertex form.
Answer
The vertex form of the equation is $$ y = (x + 4)^2 - 5 $$.
Answer for screen readers
The vertex form of the equation is $$ y = (x + 4)^2 - 5 $$.
Steps to Solve
-
Identify the quadratic equation We have the equation $y = x^2 + 8x + 11$ in standard form.
-
Complete the square To convert to vertex form, we focus on the $x^2 + 8x$ part.
-
Take the coefficient of $x$, which is 8, divide it by 2 to get 4, and then square it to get $4^2 = 16$.
-
Rewrite $x^2 + 8x$ as: $$ (x^2 + 8x + 16) - 16 $$
This maintains the equality because we added and subtracted 16.
-
-
Rewrite the equation Now substitute back into the equation: $$ y = (x^2 + 8x + 16) - 16 + 11 $$
-
Simplify the equation Simplify the constants: $$ y = (x + 4)^2 - 5 $$
-
Final vertex form The vertex form of the quadratic equation is: $$ y = (x + 4)^2 - 5 $$
The vertex form of the equation is $$ y = (x + 4)^2 - 5 $$.
More Information
In vertex form, the equation reveals that the vertex of the parabola is at the point $(-4, -5)$. This form is useful for graphing as it easily shows the vertex and the direction of the parabola.
Tips
- Forgetting to subtract the squared value when completing the square. Remember to both add and subtract the same number to keep the equation balanced.
- Not correctly simplifying the constants at the end. Always combine like terms to ensure accuracy in the final equation.
AI-generated content may contain errors. Please verify critical information