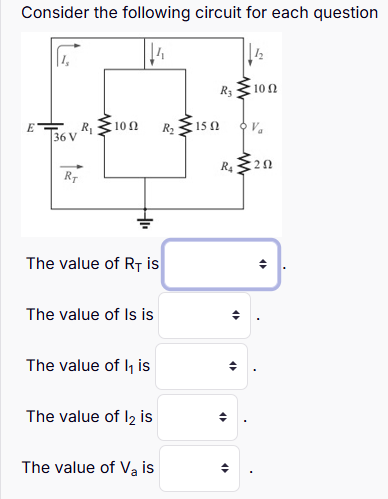
Consider the following circuit for each question: What is the value of R_T, I_s, I_1, I_2, and V_a?

Steps to Solve

1. Calculating Total Resistance (R_T)

In the given circuit, resistors $R_1$ (10 Ω) and $R_2$ (15 Ω) are in parallel. To find the equivalent resistance of parallel resistors, we use the formula: $$ \frac{1}{R_{\text{eq}}} = \frac{1}{R_1} + \frac{1}{R_2} $$

Plugging in the values: $$ \frac{1}{R_{\text{eq}}} = \frac{1}{10} + \frac{1}{15} $$

Calculating: $$ \frac{1}{R_{\text{eq}}} = \frac{3 + 2}{30} = \frac{5}{30} \implies R_{\text{eq}} = 6 , \Omega $$

Now, add the equivalent resistance $R_{\text{eq}}$ to the series resistors $R_3$ (10 Ω) and $R_4$ (2 Ω): $$ R_T = R_{\text{eq}} + R_3 + R_4 = 6 + 10 + 2 = 18 , \Omega $$

2. Finding Total Current (I_s)

We can find the source current $I_s$ using Ohm's law: $$ I_s = \frac{E}{R_T} $$

Substituting the known values: $$ I_s = \frac{36 V}{18 , \Omega} = 2 , A $$

3. Calculating Currents (I_1 and I_2)

Using the current division rule, where the total current splits between $R_1$ and $R_2$: The resistor values are 10 Ω and 15 Ω. The current division formula is: $$ I_1 = I_s \cdot \frac{R_2}{R_1 + R_2} $$ $$ I_2 = I_s \cdot \frac{R_1}{R_1 + R_2} $$

Calculating $I_1$: $$ I_1 = 2 , A \cdot \frac{15}{10 + 15} = 2 \cdot \frac{15}{25} = 2 \cdot 0.6 = 1.2 , A $$

Calculating $I_2$: $$ I_2 = 2 , A \cdot \frac{10}{10 + 15} = 2 \cdot \frac{10}{25} = 2 \cdot 0.4 = 0.8 , A $$

4. Finding Voltage (V_a)

The voltage across $R_2$ can be calculated using Ohm's law: $$ V_a = I_2 \cdot R_2 $$

Substituting in the known values: $$ V_a = 0.8 , A \cdot 15 , \Omega = 12 , V $$