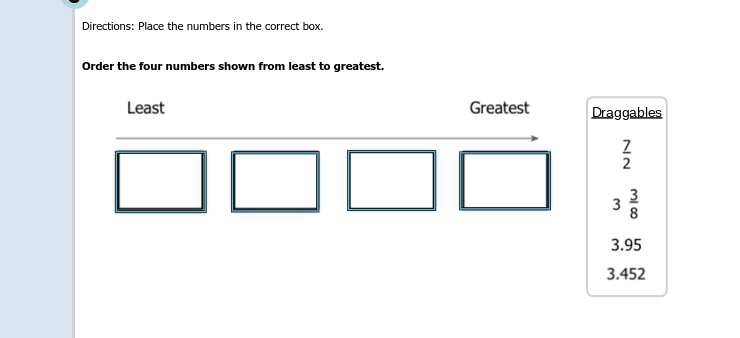
Order the four numbers shown from least to greatest: 7/2, 3/8, 3.95, 3.452.

Steps to Solve

1. Convert all numbers to decimals for easier comparison
   We have the numbers:

   • $7/2$ can be converted to decimal:
     $$ 7 \div 2 = 3.5 $$
   • $3 \frac{3}{8}$ can be converted as follows:
     First, convert $3 \frac{3}{8}$ to an improper fraction:
     $$ 3 \times 8 + 3 = 24 + 3 = 27 \quad \Rightarrow \quad \frac{27}{8} $$
     Now convert to decimal:
     $$ 27 \div 8 = 3.375 $$

2. List all the converted numbers
   Now we have the following numbers in decimal form:

   • $3.5$ from $7/2$
   • $3.375$ from $3 \frac{3}{8}$
   • $3.95$
   • $3.452$

3. Compare the decimals
   Arrange these numbers from least to greatest:

   • First, comparing $3.375$ and $3.5$, we see that $3.375 < 3.5$.
   • Next, comparing $3.452$ and $3.5$, we find that $3.452 < 3.5$.
   • Finally, $3.95$ is the largest.

4. Order the numbers
   Putting them all together in order from least to greatest:
   $$ 3.375, 3.452, 3.5, 3.95 $$