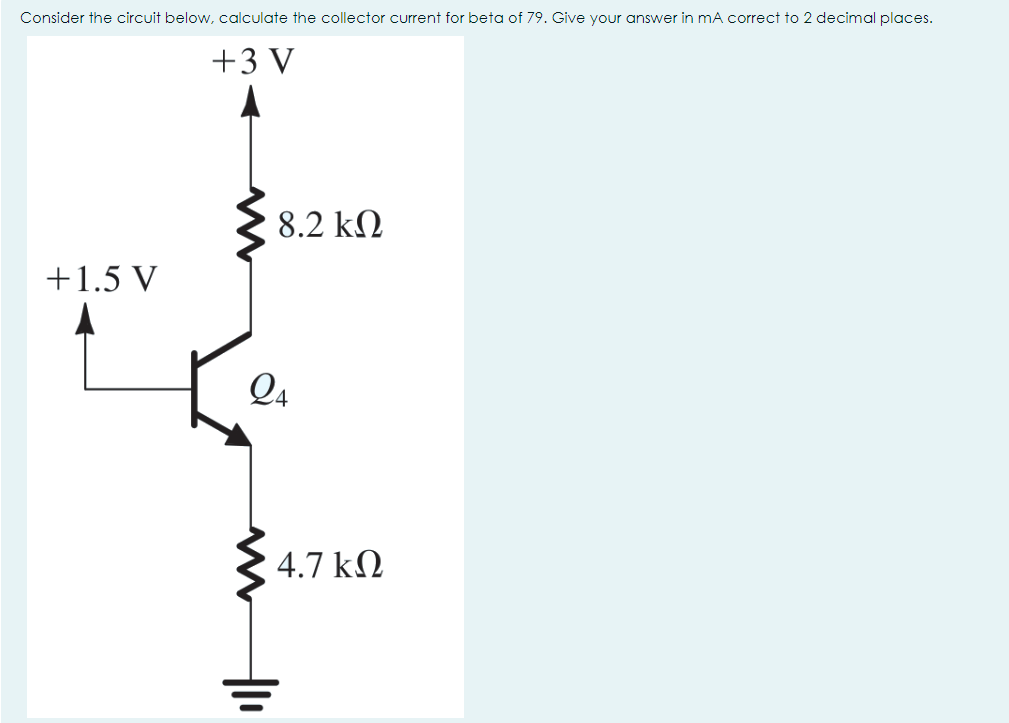
Consider the circuit below, calculate the collector current for beta of 79. Give your answer in mA correct to 2 decimal places.
Understand the Problem
The question is asking for the calculation of collector current in a transistor circuit given the beta of the transistor and the voltage values across the resistors. It requires applying circuit analysis principles to find the current in milliamperes.
Answer
The collector current is $I_C \approx 14.47 \, mA$.
Answer for screen readers
The collect current $I_C$ is approximately $14.47 , mA$.
Steps to Solve
- Calculate the Base Current ($I_B$)
To find the base current, first calculate the voltage across the 8.2 kΩ resistor. The voltage across it can be calculated using the difference between the supply voltage and the base-emitter voltage.
The voltage across the 8.2 kΩ resistor is: $$ V_B = 3V - 1.5V = 1.5V $$
Now, we can use Ohm's Law ($V = IR$) to find the base current: $$ I_B = \frac{V_B}{R_B} = \frac{1.5V}{8.2kΩ} $$
Calculating $I_B$: $$ I_B = \frac{1.5}{8200} = 0.000183 , A = 0.183 , mA $$
- Calculate the Collector Current ($I_C$)
Using the relationship between the collector current and base current with the transistor's current gain ($\beta$), we can find $I_C$: $$ I_C = \beta \times I_B = 79 \times 0.183 , mA $$
Calculating $I_C$: $$ I_C = 79 \times 0.183 = 14.467 , mA $$
- Final Calculation for Collector Current
Rounding to two decimal places: $$ I_C \approx 14.47 , mA $$
The collect current $I_C$ is approximately $14.47 , mA$.
More Information
The calculated collector current is based on the transistor's current gain (beta), which significantly amplifies the base current. Understanding how current flows in a transistor circuit allows for precise control in various electronic applications.
Tips
- Miscalculating Ohm's Law: Ensure the correct values are substituted for voltage and resistance.
- Forgetting to convert units: Remember to convert to milliamps if required.
- Using the wrong transistor parameters: Ensure beta is correctly applied.