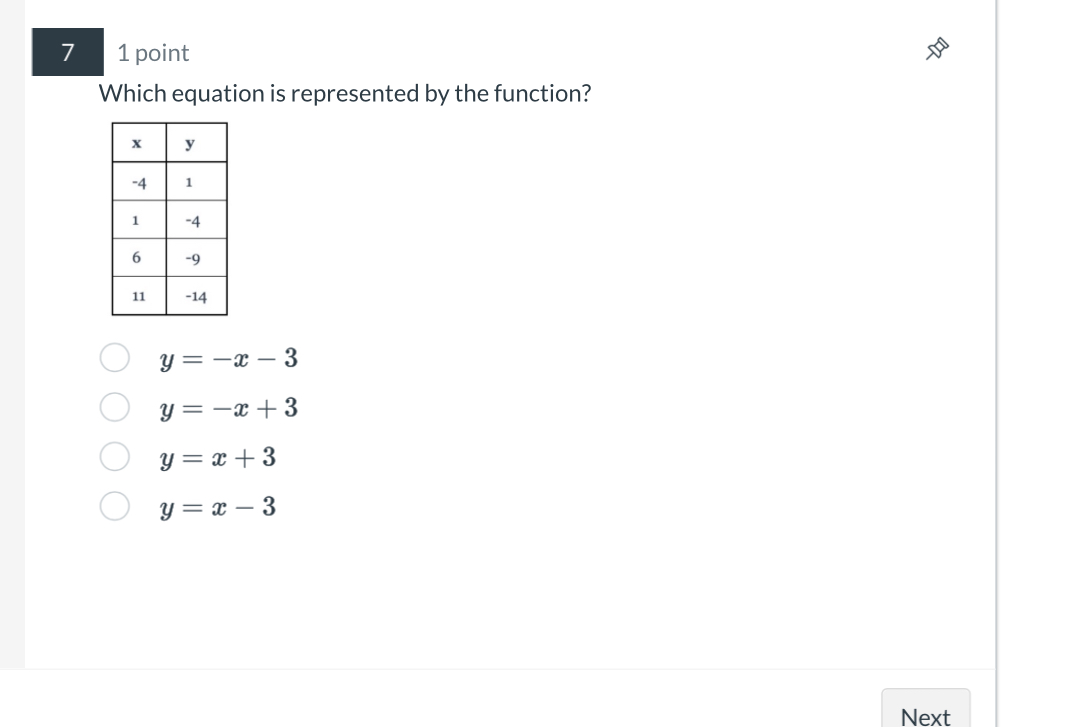
Which equation is represented by the function?

Understand the Problem

The question is asking which equation corresponds to the given set of x and y values in the table. To solve it, we need to determine the relationship between x and y from the table and see which of the provided equations matches this relationship.

Answer

$y = -x - 3$

Steps to Solve

Identify the problems with x and y values

Start by organizing the provided values from the table. The pairs are:

When $x = -4$, $y = 1$
When $x = 1$, $y = -4$
When $x = 6$, $y = -9$
When $x = 11$, $y = -14$

Calculate the slope (m) between points

To find a linear relationship, use the formula for slope:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Let's calculate the slope between the points $(-4, 1)$ and $(1, -4)$:

$$ m = \frac{-4 - 1}{1 - (-4)} = \frac{-5}{5} = -1 $$

Thus, the slope $m = -1$.

Write the equation in point-slope form

Use the point-slope form of a linear equation:

$$ y - y_1 = m(x - x_1) $$

Using point $(1, -4)$:

$$ y - (-4) = -1(x - 1) $$

Simplifying:

$$ y + 4 = -x + 1 $$

$$ y = -x + 1 - 4 $$

$$ y = -x - 3 $$

Choose the correct equation

Now compare the derived equation $y = -x - 3$ with the answer choices given:

$y = -x - 3$
$y = -x + 3$
$y = x + 3$
$y = x - 3$

The correct equation is $y = -x - 3$.

The equation represented by the function is $y = -x - 3$.

More Information

This linear equation indicates a negative slope, meaning for every unit increase in $x$, the value of $y$ decreases by 1. This matches the trend observed in the provided data points.

Tips

Confusing the slope calculation: Ensure to subtract the $y$ values and $x$ values correctly.
Not simplifying the equation correctly: Recheck steps when converting forms.

Thank you for voting!