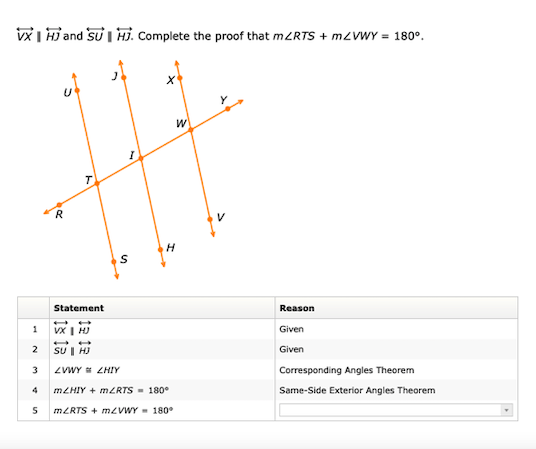
Complete the proof that m∠RTS + m∠VWY = 180°.
Understand the Problem
The question asks to complete a proof that the measures of two angles formed by two intersecting lines are supplementary, specifically that m∠RTS + m∠VWY = 180°. It involves using geometric theorems to establish the relationship between the angles created by the lines.
Answer
$$ m\angle RTS + m\angle VWY = 180^\circ $$
Answer for screen readers
The proof is complete with the conclusion: $$ m\angle RTS + m\angle VWY = 180^\circ $$
Steps to Solve
-
Identify Given Information The problem states that the lines $ \overline{VX} \parallel \overline{HJ} $ and $ \overline{SU} \parallel \overline{HJ} $ are given.
-
Establish Corresponding Angles According to the Corresponding Angles Theorem, $ \angle LWY \cong \angle LHY $ because they are corresponding angles formed by the transversal $ \overline{HY} $ intersecting the parallel lines $ \overline{VX} $ and $ \overline{HJ} $.
-
Apply the Same-Side Exterior Angles Theorem By the Same-Side Exterior Angles Theorem, we can state that: $$ m\angle LHY + m\angle RTS = 180^\circ $$ This indicates that these two angles are supplementary.
-
Final Proof Statement From the established step above, we substitute to show: $$ m\angle RTS + m\angle VWY = 180^\circ $$ Thus completing the proof.
The proof is complete with the conclusion: $$ m\angle RTS + m\angle VWY = 180^\circ $$
More Information
This proof uses the properties of parallel lines and angles formed by transversals, demonstrating how geometry relies on established theorems to establish relationships between angles.
Tips
- Misidentifying the types of angles formed by intersecting lines can lead to incorrect conclusions about their relationships.
- Forgetting to state or apply the appropriate geometric theorem can result in gaps in the proof.
AI-generated content may contain errors. Please verify critical information