Combine like terms: x^2 + 4 + 5y^3 + 2x^2 - 2x^2 - 6 + 1.
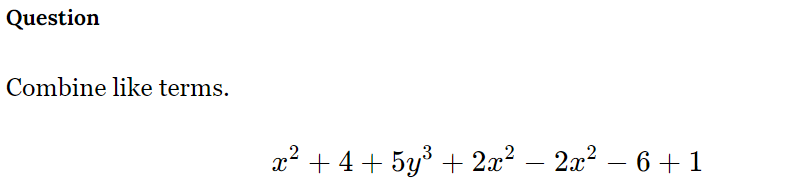
Understand the Problem
The question is asking us to combine like terms from the given polynomial expression. This involves identifying and summing up the coefficients of the terms that have the same variable and exponent.
Answer
The combined expression is $x^2 + 5y^3 - 1$.
Answer for screen readers
The combined expression is:
$$ x^2 + 5y^3 - 1 $$
Steps to Solve
- Identify the like terms
In the expression, collect all terms having the same variable and exponent. The terms are:
- For $x^2$: $x^2$, $2x^2$, and $-2x^2$.
- For $y^3$: $5y^3$.
- For constant terms: $4$, $-6$, and $1$.
- Combine the like terms for $x^2$
Add the coefficients of $x^2$:
$$1 + 2 - 2 = 1$$
So, the combined term for $x^2$ is $1x^2$ or simply $x^2$.
- Write the remaining like terms
Summarize the other like terms:
- The term for $y^3$ remains as $5y^3$.
- For constants:
$$4 - 6 + 1 = -1$$
- Combine all terms into a single expression
Combine the results from above:
$$x^2 + 5y^3 - 1$$
Thus, the simplified expression is $x^2 + 5y^3 - 1$.
The combined expression is:
$$ x^2 + 5y^3 - 1 $$
More Information
Combining like terms helps simplify polynomials, making them easier to work with. This process is foundational in algebra and is used in various applications, including solving equations and graphing.
Tips
- Forgetting to include all like terms: Always double-check that all similar terms have been combined.
- Miscalculating when adding or subtracting coefficients: Pay careful attention to the signs of the coefficients.
AI-generated content may contain errors. Please verify critical information