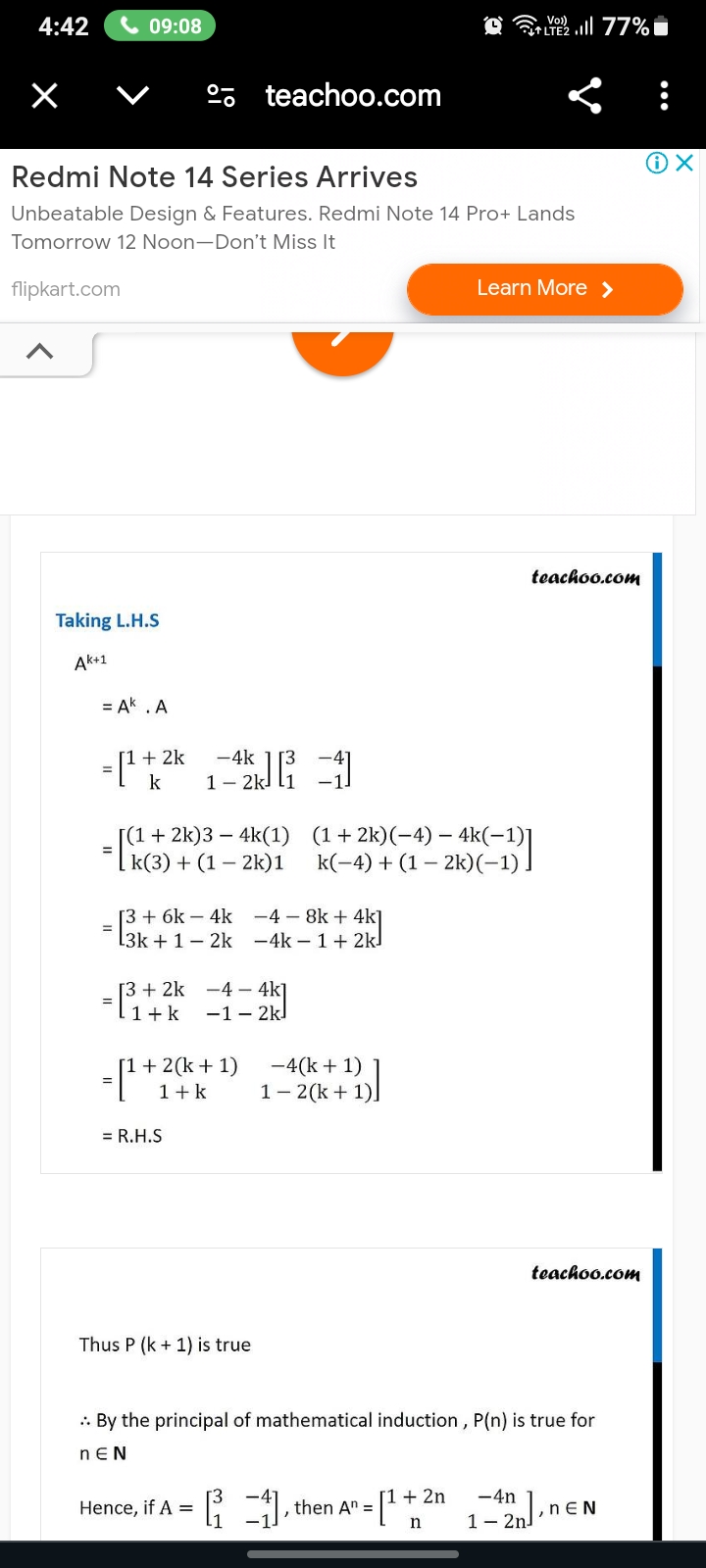
Taking L.H.S A^(k+1) = A^k . A = ... thus P(k + 1) is true. By the principle of mathematical induction, P(n) is true for n ∈ N

Steps to Solve

1. Setting up the Left-Hand Side (LHS) We start with the expression for ( A^{k+1} ): $$ A^{k+1} = A^k \cdot A = \begin{bmatrix} 1 + 2k & -4k \ 1 - 2k & 1 \end{bmatrix} \cdot \begin{bmatrix} 3 & -4 \ 1 & -1 \end{bmatrix} $$

2. Matrix Multiplication Multiply the two matrices: $$ = \begin{bmatrix} (1 + 2k)3 + (-4k)(1) & (1 + 2k)(-4) + (-4k)(-1) \ (1 - 2k)3 + 1(-4) & (1 - 2k)(-4) + 1(-1) \end{bmatrix} $$

3. Calculating Each Element Calculate each element in the resulting matrix:

   • First row, first element: $$ 3 + 6k - 4k = 3 + 2k $$
   • First row, second element: $$ -4 - 8k + 4k = -4 - 4k $$
   • Second row, first element: $$ 3 - 6k - 4 = -1 - 2k $$
   • Second row, second element: $$ -4 + 2k - 1 = -5 + 2k $$

4. Representing the Result The resulting matrix is: $$ \begin{bmatrix} 3 + 2k & -4 - 4k \ -1 - 2k & -5 + 2k \end{bmatrix} $$

5. Showing it Equals the Right-Hand Side (RHS) We need to show: $$ \begin{bmatrix} 1 + 2(k+1) & -4(k+1) \ 1 + k + 1 & 1 - 2(k+1) \end{bmatrix} $$ This simplifies to: $$ \begin{bmatrix} 1 + 2k + 2 & -4k - 4 \ 1 + k + 1 & 1 - 2k - 2 \end{bmatrix} = \begin{bmatrix} 3 + 2k & -4 - 4k \ 2 + k & -1 - 2k \end{bmatrix} $$

6. Conclusion of Induction Step Since LHS equals RHS, we conclude: ( P(k+1) ) is true, thus by induction ( P(n) ) holds for all ( n \in \mathbb{N} ).