Combine like terms: -6 - 2y² - 3 + 3y - 2y² + 4y + 6y²
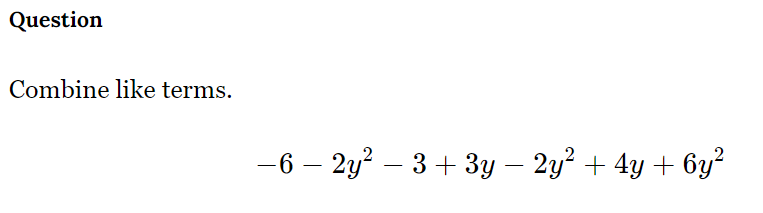
Understand the Problem
The question is asking to combine like terms in the given algebraic expression, which involves grouping similar variables together and simplifying the expression accordingly.
Answer
The simplified expression is: $$ -9 + 2y^2 + 6y $$
Answer for screen readers
The simplified expression is:
$$ -9 + 2y^2 + 6y $$
Steps to Solve
- Group like terms
Identify and group the like terms in the expression. Here we have:
- Constants: $-6$, $-3$
- $y^2$ terms: $-2y^2$, $-2y^2$, $6y^2$
- $y$ terms: $3y$, $4y$, $-y$
- Combine the constants
Now sum the constants:
$$ -6 - 3 = -9 $$
- Combine the $y^2$ terms
Next, sum the $y^2$ terms:
$$ -2y^2 - 2y^2 + 6y^2 = (6 - 2 - 2)y^2 = 2y^2 $$
- Combine the $y$ terms
Then sum the $y$ terms:
$$ 3y + 4y - y = (3 + 4 - 1)y = 6y $$
- Write the final expression
The final expression, after combining all like terms, is:
$$ -9 + 2y^2 + 6y $$
The simplified expression is:
$$ -9 + 2y^2 + 6y $$
More Information
This process of combining like terms is fundamental in algebra, allowing for simplification of expressions and easier manipulation in equations. It's crucial for solving equations and performing polynomial operations.
Tips
- Misidentifying like terms: Ensure that the terms have the same variable and exponent.
- Sign errors: Be cautious with negative signs when combining terms; they can often lead to incorrect totals.
AI-generated content may contain errors. Please verify critical information