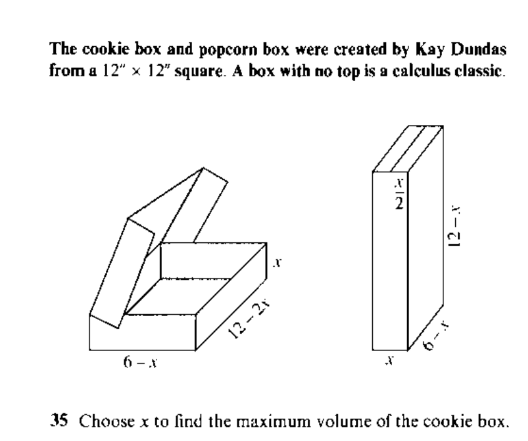
Choose x to find the maximum volume of the cookie box.

Steps to Solve

1. Define the Volume Equation The volume ( V ) of the box can be expressed in terms of ( x ) (the height of the box) as follows:

The base of the box has dimensions:

• Length = ( 12 - 2x ) (since ( x ) is cut from both ends)
• Width = ( 12 - 2x )

Thus, the volume can be calculated using the formula: $$ V = \text{Length} \times \text{Width} \times \text{Height} = (12 - 2x)(12 - 2x)(x) $$

2. Simplify the Volume Equation Now we need to simplify the expression for the volume ( V ):

Start by expanding: $$ V = x(12 - 2x)^2 = x(144 - 48x + 4x^2) $$

This leads to: $$ V = 144x - 48x^2 + 4x^3 $$

3. Differentiate the Volume Function To find the maximum volume, we need to find the derivative of ( V ) with respect to ( x ): $$ \frac{dV}{dx} = 144 - 96x + 12x^2 $$

4. Set the Derivative to Zero Setting the derivative equal to zero to find the critical points: $$ 12x^2 - 96x + 144 = 0 $$

5. Solve the Quadratic Equation Dividing the entire equation by 12 simplifies it to: $$ x^2 - 8x + 12 = 0 $$

Now factor or use the quadratic formula. The roots are found with: $$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{8 \pm \sqrt{(-8)^2 - 4 \cdot 1 \cdot 12}}{2 \cdot 1} $$ $$ x = \frac{8 \pm \sqrt{64 - 48}}{2} = \frac{8 \pm \sqrt{16}}{2} = \frac{8 \pm 4}{2} $$

Thus: $$ x = \frac{12}{2} = 6 \quad \text{or} \quad x = \frac{4}{2} = 2 $$

6. Determine Which Critical Point Maximizes the Volume Evaluate the second derivative test or plug values back into the original volume equation to confirm which ( x ) gives the maximum volume.

If ( x = 6 ):

• The dimensions will be negative, thus invalid.

If ( x = 2 ):

• The dimensions will be positive and valid.

7. Calculate the Maximum Volume Substituting ( x = 2 ) back into the volume formula: $$ V = 144(2) - 48(2^2) + 4(2^3) $$ $$ V = 288 - 192 + 32 = 128 $$