Choose Athena's correct distance travelled and displacement from the drop-down menu.
Understand the Problem
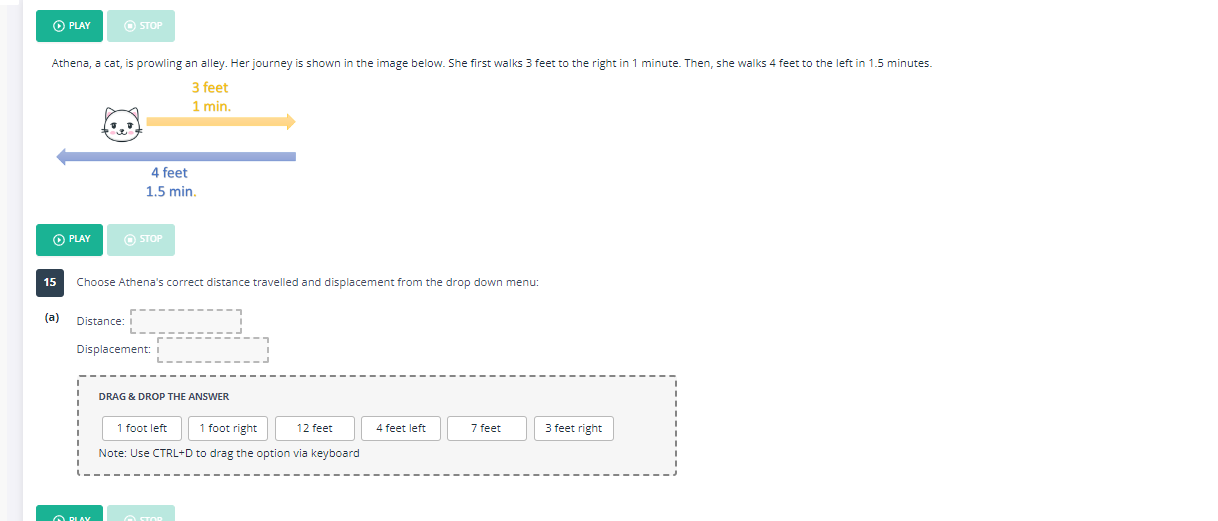
The question is asking for the total distance Athena the cat has traveled and her overall displacement after moving in two different directions. It involves calculating the total distance moved and the net change in position.
Answer
Distance: 7 feet, Displacement: 1 foot left.
Answer for screen readers
Distance: 7 feet
Displacement: 1 foot left
Steps to Solve
- Calculate Total Distance Traveled
To find the total distance Athena has traveled, we add the distances of each segment of her journey.
- Distance to the right: 3 feet
- Distance to the left: 4 feet
The total distance is calculated as follows:
$$ \text{Total Distance} = 3 , \text{feet} + 4 , \text{feet} = 7 , \text{feet} $$
- Calculate Overall Displacement
Displacement is the net change in position, taking direction into account. Since Athena moves 3 feet to the right and then 4 feet to the left, we represent right as positive and left as negative:
- Position after first movement: +3 feet
- Position after second movement: -4 feet
The overall displacement is calculated as follows:
$$ \text{Displacement} = 3 , \text{feet} - 4 , \text{feet} = -1 , \text{foot} $$
This means she is 1 foot left from her starting position.
Distance: 7 feet
Displacement: 1 foot left
More Information
Athena's total distance traveled is the sum of all the parts of her journey, regardless of direction. However, displacement only considers the starting and ending points, with direction playing a significant role.
Tips
- Confusing distance with displacement: Remember that distance is always positive and adds up all traveled segments, while displacement takes direction into account.
- Forgetting to check signs for displacement: Make sure to give appropriate signs (+ for right, - for left) when calculating net movement.
AI-generated content may contain errors. Please verify critical information