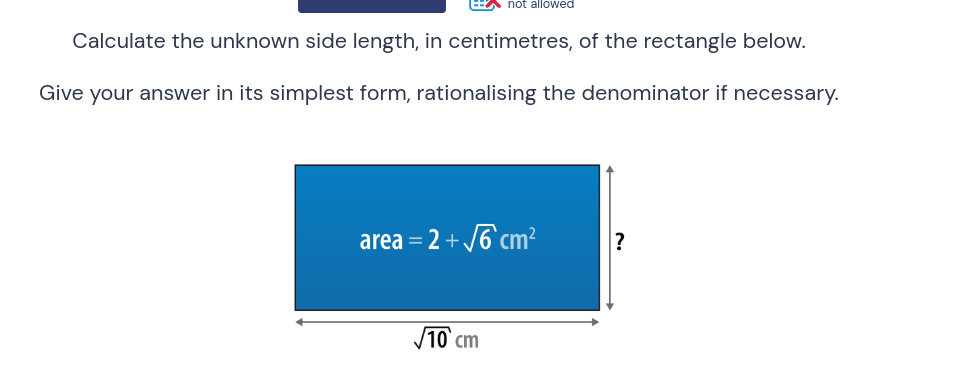
Calculate the unknown side length, in centimetres, of the rectangle below. Give your answer in its simplest form, rationalising the denominator if necessary.

Steps to Solve

1. Identify Information Given The area of the rectangle is given as ( A = 2 + \sqrt{6} , \text{cm}^2 ) and one side length is ( \sqrt{10} , \text{cm} ).

2. Use the Area Formula The area of a rectangle is calculated using the formula: $$ A = \text{length} \times \text{width} $$ Let the unknown side length be ( x ). Substitute the known values into the formula: $$ 2 + \sqrt{6} = \sqrt{10} \cdot x $$

3. Solve for the Unknown Side Length To isolate ( x ), divide both sides by ( \sqrt{10} ): $$ x = \frac{2 + \sqrt{6}}{\sqrt{10}} $$

4. Rationalize the Denominator To rationalize the denominator, multiply the numerator and denominator by ( \sqrt{10} ): $$ x = \frac{(2 + \sqrt{6})\sqrt{10}}{10} $$

5. Simplify the Expression Expand the numerator: $$ x = \frac{2\sqrt{10} + \sqrt{60}}{10} $$

6. Further Simplify ( \sqrt{60} ) Since ( \sqrt{60} = \sqrt{4 \cdot 15} = 2\sqrt{15} ), substitute this back: $$ x = \frac{2\sqrt{10} + 2\sqrt{15}}{10} $$

7. Final Simplification Factor out the common factor in the numerator: $$ x = \frac{2(\sqrt{10} + \sqrt{15})}{10} $$

Then simplify: $$ x = \frac{\sqrt{10} + \sqrt{15}}{5} $$