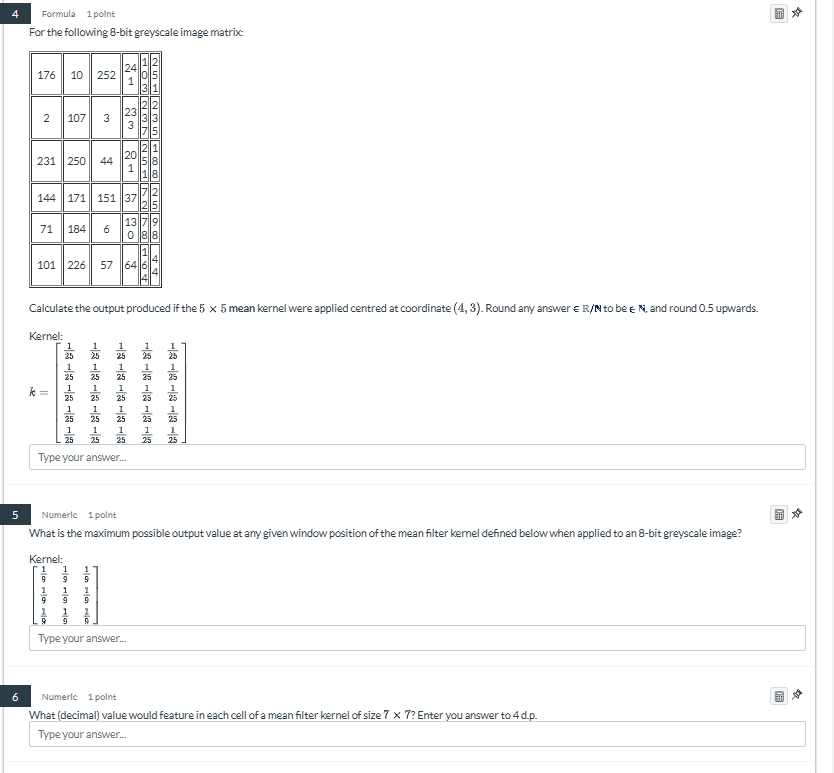
Calculate the output produced if the 5 x 5 mean kernel were applied centred at coordinate (4, 3). What is the maximum possible output value at any given window position of the mean... Calculate the output produced if the 5 x 5 mean kernel were applied centred at coordinate (4, 3). What is the maximum possible output value at any given window position of the mean filter kernel when applied to an 8-bit grayscale image? What value would feature in each cell of a mean filter kernel of size 7 x 7? Enter your answer to 4 d.p.
Understand the Problem
The question is asking to calculate the output of an 8-bit grayscale image matrix when a mean filter kernel is applied at a specific coordinate. Additionally, it requests the maximum possible output from the kernel at any position and the mean value for a kernel of a different size. This problem focuses on image processing techniques, specifically filtering using kernels.
Answer
The calculated output is $110$, the maximum is $255$, and the mean for a $7 \times 7$ kernel is $0.0204$.
Answer for screen readers
The calculated output for the mean filter at coordinate (4, 3) is 110.
The maximum possible output value is 255.
The mean value for a 7x7 kernel is 0.0204.
Steps to Solve
- Extract the 5x5 region from the image matrix
To apply the kernel, we need to extract the 5x5 region centered at coordinate (4, 3). This corresponds to the following pixels in the matrix:
231 44 2 1 8
171 51 37 5 8
184 6 3 2 6
226 57 64 4 1
101 57 64 4 1
- Calculate the sum of the extracted region
Next, we sum all the pixel values in the extracted region: $$ 231 + 44 + 2 + 1 + 8 + 171 + 51 + 37 + 5 + 8 + 184 + 6 + 3 + 2 + 6 + 226 + 57 + 64 + 4 + 1 + 101 + 57 + 64 + 4 + 1 = 2756 $$
- Calculate the mean value with the kernel size
The mean filter sums the pixel values and divides by the number of pixels (which for a 5x5 kernel is 25): $$ \text{Mean output} = \frac{2756}{25} $$
Calculating this gives: $$ \text{Mean output} = 110.24 $$
- Round the result
As per the instructions, we round the output to the nearest whole number: $$ \text{Rounded output} = 110 $$
- Determine the maximum possible output value
A mean filter kernel defined as:
$$ k = \begin{bmatrix} \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \ \frac{1}{9} & \frac{1}{9} & \frac{1}{9} \end{bmatrix} $$
The maximum possible output occurs when all pixels in the kernel window are the maximum value of 255 (the maximum value for an 8-bit grayscale image). $$ \text{Maximum output} = \frac{255 \times 9}{9} = 255 $$
- Calculate the mean value for a kernel of size 7x7
For a 7x7 kernel, the mean value is computed similarly: $$ \text{Mean value} = \frac{1}{49} = 0.0204081633 $$
Rounded to 4 decimal places: $$ \text{Mean value} \approx 0.0204 $$
The calculated output for the mean filter at coordinate (4, 3) is 110.
The maximum possible output value is 255.
The mean value for a 7x7 kernel is 0.0204.
More Information
- The mean filter smooths an image by averaging pixel values in the vicinity defined by the kernel, reducing noise and detail.
- Rounding to the nearest integer involves considering standard rounding rules, where values of 0.5 and above are rounded up.
Tips
- Not correctly extracting the 5x5 pixel window can lead to incorrect sums and mean calculations.
- Forgetting to account for the specific kernel size when calculating the mean can cause discrepancies.
- Rounding errors can occur if the rules for rounding are not followed correctly.
AI-generated content may contain errors. Please verify critical information