Fully factorise n² + 4n - 32
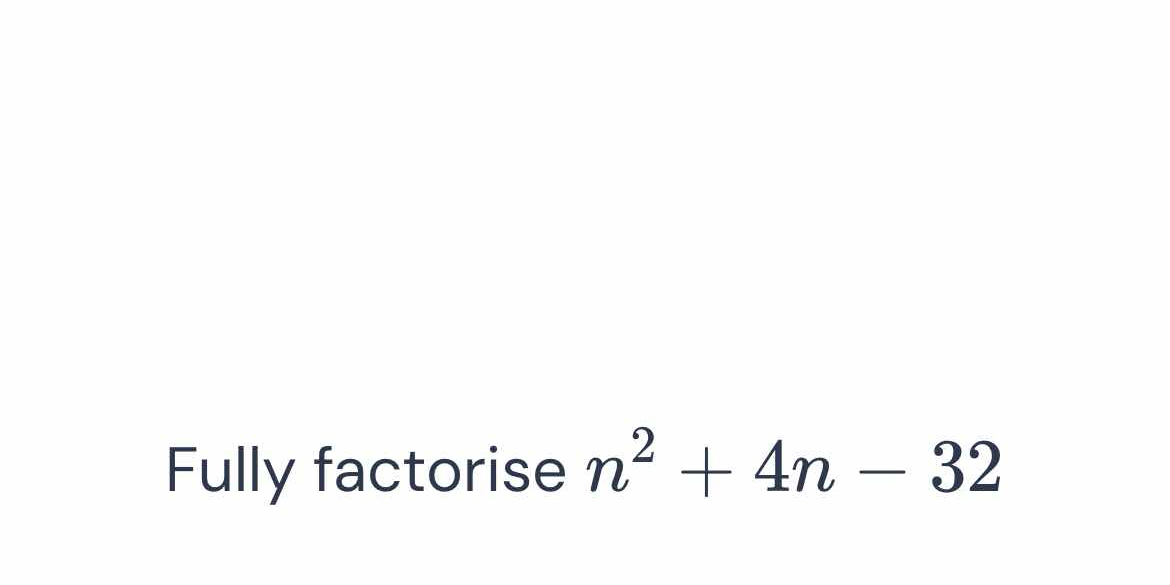
Understand the Problem
The question asks to fully factor the quadratic expression n² + 4n - 32. This involves finding two binomials that, when multiplied together, give the original expression. The key concepts include identifying factors of -32 that add up to 4.
Answer
The fully factored form is \( (n + 8)(n - 4) \).
Answer for screen readers
The fully factored form of the expression ( n^2 + 4n - 32 ) is ( (n + 8)(n - 4) ).
Steps to Solve
- Identify the quadratic expression
We start with the quadratic expression ( n^2 + 4n - 32 ).
- Find factors of the constant term
We need to find two numbers that multiply to (-32) (the constant term) and add up to (4) (the coefficient of (n)).
- List the pairs of factors of -32
The factor pairs of (-32) are:
- ( 1 \times -32 )
- ( -1 \times 32 )
- ( 2 \times -16 )
- ( -2 \times 16 )
- ( 4 \times -8 )
- ( -4 \times 8 )
- Select the correct factor pair
The pair that adds up to (4) is (8) and (-4): [ 8 + (-4) = 4 ]
- Write the expression as binomials
Using the factors found, we can express ( n^2 + 4n - 32 ) as: [ (n + 8)(n - 4) ]
- Final factorization
Thus, the fully factored form of the quadratic expression is: [ n^2 + 4n - 32 = (n + 8)(n - 4) ]
The fully factored form of the expression ( n^2 + 4n - 32 ) is ( (n + 8)(n - 4) ).
More Information
Factoring quadratics is a useful skill in algebra that can help simplify expressions and solve equations more easily. The process involves identifying factors that meet specific addition and multiplication criteria related to the expression.
Tips
- Misidentifying the signs of the factors (a negative and positive pair must be correctly chosen).
- Not considering all possible factor pairs of the constant term.
- Forgetting to double-check that both the sum and product conditions are satisfied.
AI-generated content may contain errors. Please verify critical information