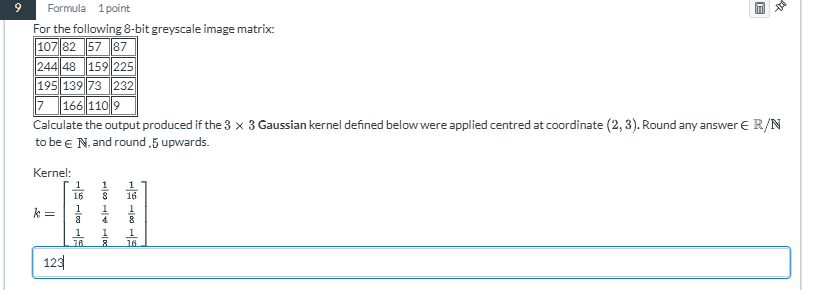
Calculate the output produced if the 3 × 3 Gaussian kernel defined below were applied centred at coordinate (2, 3). Round any answer to be in ℝ/N to be ℕ, and round .5 upwards. Calculate the output produced if the 3 × 3 Gaussian kernel defined below were applied centred at coordinate (2, 3). Round any answer to be in ℝ/N to be ℕ, and round .5 upwards.
Understand the Problem
The question asks us to calculate the output of a Gaussian kernel applied to a specific part of a grayscale image matrix. It requires applying the kernel to the pixel values around the coordinate (2, 3), summing them up, and rounding the result according to specified rules.
Answer
The output of the Gaussian kernel at (2, 3) is 126.
Answer for screen readers
The output of the Gaussian kernel at coordinate (2, 3) is 126.
Steps to Solve
-
Extract the pixel values around (2, 3)
The position (2, 3) in the image matrix corresponds to the pixel value:- (1, 2) = 48
- (1, 3) = 159
- (1, 4) = 225
- (2, 2) = 139
- (2, 3) = 73
- (2, 4) = 232
- (3, 2) = 166
- (3, 3) = 110
Therefore, the relevant pixel values are: $$ \begin{matrix} 48 & 159 & 225 \ 139 & 73 & 232 \ 166 & 110 & 0 \ \end{matrix} $$ (Note: The last value in row 3, column 4 is considered zero or ignored as it is out of range)
-
Multiply with the Gaussian kernel
We multiply each pixel value by the corresponding value in the kernel, which is given by: $$ k = \begin{matrix} \frac{1}{16} & \frac{1}{8} & \frac{1}{16} \ \frac{1}{8} & \frac{1}{4} & \frac{1}{8} \ \frac{1}{16} & \frac{1}{8} & \frac{1}{16} \ \end{matrix} $$ After applying the kernel, we have: $$ \text{Weighted values} = \begin{matrix} 48 \cdot \frac{1}{16} & 159 \cdot \frac{1}{8} & 225 \cdot \frac{1}{16} \ 139 \cdot \frac{1}{8} & 73 \cdot \frac{1}{4} & 232 \cdot \frac{1}{8} \ 166 \cdot \frac{1}{16} & 110 \cdot \frac{1}{8} & 0 \cdot \frac{1}{16} \ \end{matrix} $$ -
Calculate the weighted pixel values
Calculate the individual contributions:- ( 48 \times \frac{1}{16} = 3 )
- ( 159 \times \frac{1}{8} = 19.875 )
- ( 225 \times \frac{1}{16} = 14.0625 )
- ( 139 \times \frac{1}{8} = 17.375 )
- ( 73 \times \frac{1}{4} = 18.25 )
- ( 232 \times \frac{1}{8} = 29 )
- ( 166 \times \frac{1}{16} = 10.375 )
- ( 110 \times \frac{1}{8} = 13.75 )
-
Sum the weighted values
Now, we sum all the contributions: $$ 3 + 19.875 + 14.0625 + 17.375 + 18.25 + 29 + 10.375 + 13.75 = 125.6875 $$ -
Round the result
Following the given instruction to round up:- Round ( 125.6875 ) to the nearest whole number results in ( 126 ).
The output of the Gaussian kernel at coordinate (2, 3) is 126.
More Information
This process involves the convolution of an image with a Gaussian kernel, which is commonly used in image processing to apply a blurring effect. The kernel weights pixels based on their proximity to the pixel being processed.
Tips
- Ignoring out-of-bounds pixels: Ensure that you only apply the kernel within the bounds of the image.
- Mistakes in multiplication: Carefully calculate the product of the pixel values and their corresponding kernel weights.
- Incorrect rounding: Make sure to round correctly, following the provided rounding guidelines.
AI-generated content may contain errors. Please verify critical information