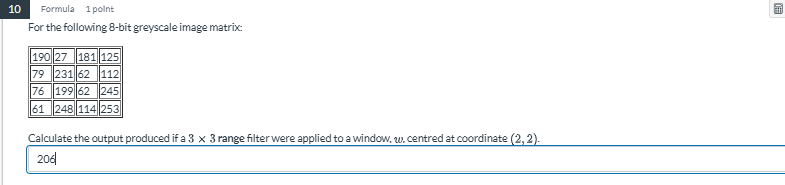
Calculate the output produced if a 3 x 3 range filter were applied to a window, centered at coordinate (2, 2).

Understand the Problem

The question is asking to calculate the output of a 3x3 range filter applied to a specified window on an 8-bit greyscale image matrix centered at the coordinate (2, 2). This requires understanding how to apply the filter and calculate the appropriate value based on the matrix values surrounding that coordinate.

Answer

$186$

Steps to Solve

Identify the 3x3 Window

The center coordinate is (2, 2). The 3x3 window includes the pixels surrounding this coordinate. The pixels involved are:
```
[
[ 181, 125, 231 ],
[ 62,  112,  199 ],
[ 114, 245, 248 ]
]
```
Extract Pixel Values

Extract the values of the pixels from the window:
- Row 1: 181, 125, 231
- Row 2: 62, 112, 199
- Row 3: 114, 245, 248
Calculate the Minimum and Maximum Values

Determine the minimum and maximum values from the selected pixel values:
- Minimum: $ \text{min}(181, 125, 231, 62, 112, 199, 114, 245, 248) = 62 $
- Maximum: $ \text{max}(181, 125, 231, 62, 112, 199, 114, 245, 248) = 248 $
Calculate the Output Using the Range Filter

The equation for the output is given by: $$ \text{output} = \text{max} - \text{min} $$

Substitute the minimum and maximum values: $$ \text{output} = 248 - 62 = 186 $$

The output produced by the 3x3 range filter is $186$.

More Information

The range filter calculates output based on the spread of pixel values within a window. It is useful in enhancing image features by highlighting areas of significant contrast or detail.

Tips

Incorrect Window Selection: Ensure the 3x3 window is correctly centered on the specified coordinate.
Min/Max Calculation Errors: Double-check calculations for minimum and maximum values to avoid incorrect outputs.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!