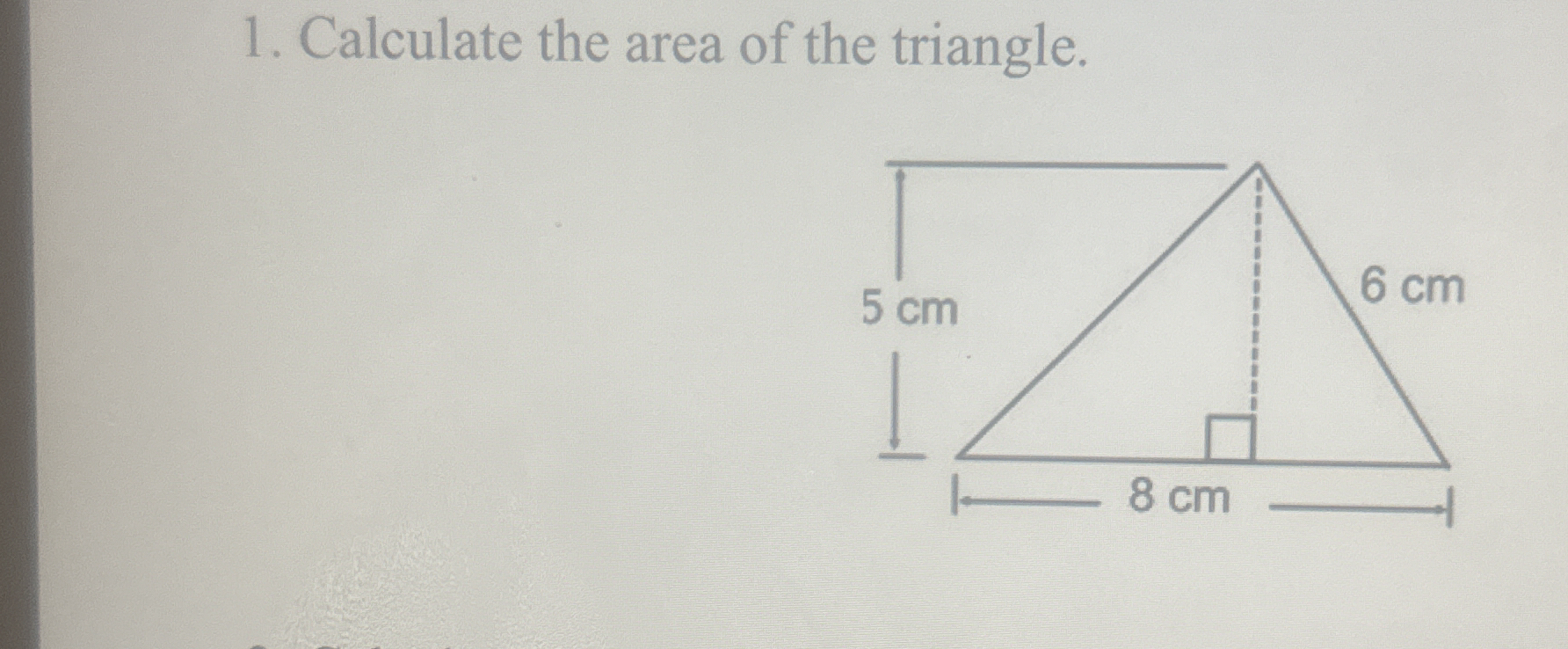
Calculate the area of the triangle.
Understand the Problem
The question is asking to calculate the area of a triangle given its dimensions: base of 8 cm and height of 5 cm.
Answer
The area of the triangle is \(20 \, \text{cm}^2\).
Answer for screen readers
The area of the triangle is (20 , \text{cm}^2).
Steps to Solve
- Identify the formula for the area of a triangle
The area (A) of a triangle can be calculated using the formula: $$ A = \frac{1}{2} \times \text{base} \times \text{height} $$
- Substitute the given values into the formula
In this problem, the base is (8 , \text{cm}) and the height is (5 , \text{cm}). Substitute these values into the formula: $$ A = \frac{1}{2} \times 8 \times 5 $$
- Calculate the area
Now perform the calculations step-by-step: First, calculate the product of the base and height: $$ 8 \times 5 = 40 $$
Then, multiply by (\frac{1}{2}): $$ A = \frac{1}{2} \times 40 = 20 $$
The area of the triangle is (20 , \text{cm}^2).
More Information
The area of a triangle can be thought of as half the product of its base and height. This formula applies to all triangles, irrespective of their shape, as long as you know the base and the height.
Tips
- Forgetting the (\frac{1}{2}) in the area formula can lead to calculating the entire rectangle formed by the base and height. To avoid this, always remember that the area of a triangle is half that of a rectangle.
AI-generated content may contain errors. Please verify critical information