∫ sec(u) / tan²(u) du
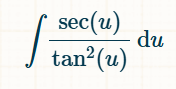
Understand the Problem
The question is asking us to evaluate the integral of the function sec(u) divided by tan^2(u) with respect to u. This involves using integration techniques, possibly including trigonometric identities.
Answer
The integral evaluates to $-\cot(u) - u + C$.
Answer for screen readers
The final answer to the integral is:
$$ -\cot(u) - u + C $$
Steps to Solve
- Rewrite the integral using trigonometric identities
We know that $\sec(u) = \frac{1}{\cos(u)}$ and $\tan(u) = \frac{\sin(u)}{\cos(u)}$. Thus, we can rewrite the integral as:
$$ \int \frac{\sec(u)}{\tan^2(u)} , du = \int \frac{1/\cos(u)}{(\sin(u)/\cos(u))^2} , du = \int \frac{\cos^2(u)}{\sin^2(u)} , du $$
- Simplify the expression
This simplifies to:
$$ \int \cot^2(u) , du $$
- Use a known integral formula
Recalling that $\cot^2(u) = \csc^2(u) - 1$, we can split the integral:
$$ \int \cot^2(u) , du = \int (\csc^2(u) - 1) , du $$
- Evaluate the integral
Now we can integrate each term separately:
$$ \int \csc^2(u) , du - \int 1 , du $$
Using the known integrals, we have:
$$ -\cot(u) - u + C $$
where $C$ is the constant of integration.
The final answer to the integral is:
$$ -\cot(u) - u + C $$
More Information
This integral utilizes the properties of trigonometric functions and their relationships, particularly the identities of cotangent and cosecant. The result, $-\cot(u) - u + C$, combines the integration of cotangent and simple linear integration.
Tips
- Ignoring Trigonometric Identities: Students often forget to apply trigonometric identities correctly when rewriting expressions. It's important to be comfortable with basic identities like $\cot^2(u) + 1 = \csc^2(u)$.
- Not Simplifying Before Integrating: Some may try to integrate the original functions without first simplifying. Simplifying can make the integral much easier to solve.
AI-generated content may contain errors. Please verify critical information