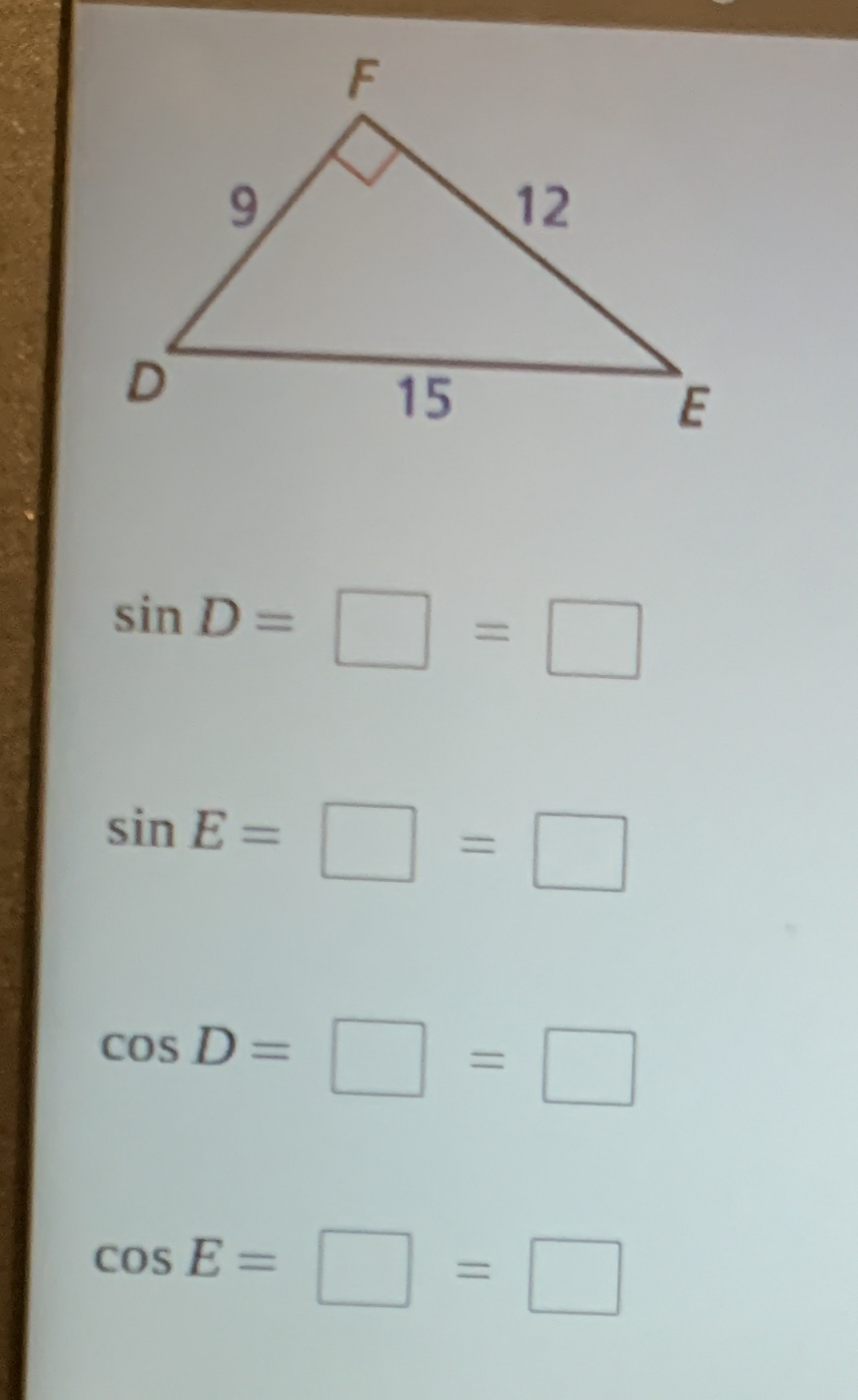
Calculate sin D, sin E, cos D, and cos E for the given triangle.

Understand the Problem

The question is asking to calculate the sine and cosine values for angles D and E in the given triangle based on its side lengths using trigonometric functions. It involves applying the definitions of sine and cosine in the context of triangles.

Answer

- $ \sin D = \frac{4}{5} $, $ \sin E = \frac{3}{5} $ - $ \cos D = \frac{3}{5} $, $ \cos E = \frac{4}{5} $

Steps to Solve

Identify Triangle Sides and Angles

From the triangle, we have the lengths of the sides:

( a = 12 ) (opposite angle ( D ))
( b = 9 ) (opposite angle ( E ))
( c = 15 ) (the side opposite the right angle at ( F ))

Use the Sine Function

The sine of an angle in a right triangle is defined as the ratio of the length of the opposite side to the hypotenuse.

For angle ( D ): $$ \sin D = \frac{\text{opposite side to } D}{\text{hypotenuse}} = \frac{12}{15} $$

For angle ( E ): $$ \sin E = \frac{\text{opposite side to } E}{\text{hypotenuse}} = \frac{9}{15} $$

Simplify the Sine Values

Now, let's simplify these fractions:

For ( \sin D ): $$ \sin D = \frac{12}{15} = \frac{4}{5} $$
For ( \sin E ): $$ \sin E = \frac{9}{15} = \frac{3}{5} $$

Use the Cosine Function

The cosine of an angle is defined as the ratio of the length of the adjacent side to the hypotenuse.

For angle ( D ): $$ \cos D = \frac{\text{adjacent side to } D}{\text{hypotenuse}} = \frac{9}{15} $$

For angle ( E ): $$ \cos E = \frac{\text{adjacent side to } E}{\text{hypotenuse}} = \frac{12}{15} $$

Simplify the Cosine Values

Simplifying these fractions gives:

For ( \cos D ): $$ \cos D = \frac{9}{15} = \frac{3}{5} $$
For ( \cos E ): $$ \cos E = \frac{12}{15} = \frac{4}{5} $$

( \sin D = \frac{4}{5} )
( \sin E = \frac{3}{5} )
( \cos D = \frac{3}{5} )
( \cos E = \frac{4}{5} )

More Information

These trigonometric functions describe the relationships between the sides of a right triangle and can be used in various applications in physics, engineering, and mathematics, particularly in solving problems involving angles and distances.

Tips

Confusing the opposite and adjacent sides when applying sine and cosine functions. Remember that sine is always opposite over hypotenuse, and cosine is adjacent over hypotenuse.
Not simplifying fractions correctly.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!