c) -\frac{2}{3}h^{3} \times \frac{5}{9}h^{-5}
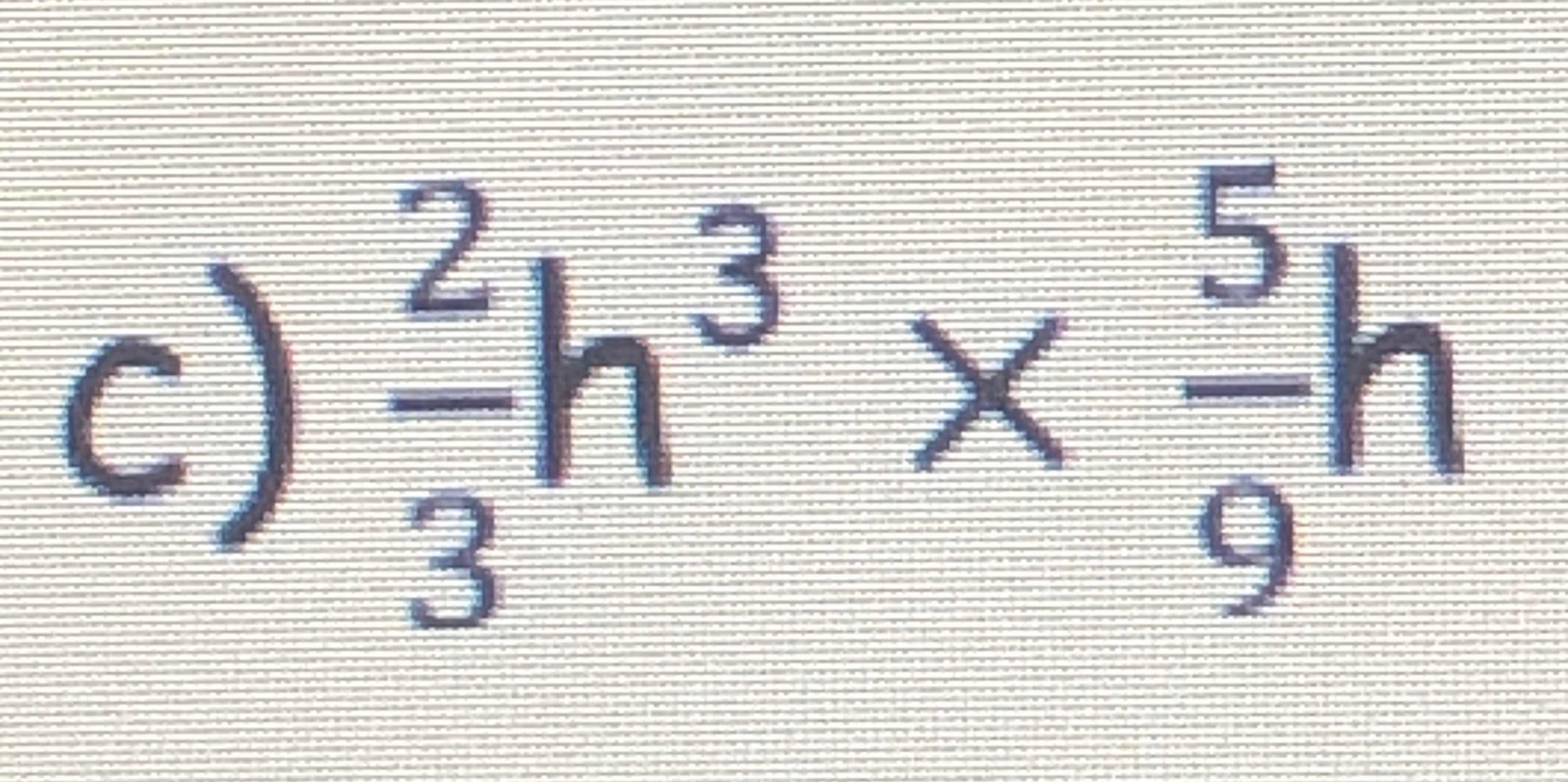
Understand the Problem
The question appears to involve a mathematical expression that involves the variable h raised to different powers and multiplied together. It likely requires simplification or evaluation.
Answer
The answer is $$ -\frac{10}{27h^{2}} $$.
Answer for screen readers
The final simplified answer is: $$ -\frac{10}{27h^{2}} $$
Steps to Solve
- Multiply the coefficients To start, multiply the numerical coefficients together. We have: $$ -\frac{2}{3} \times \frac{5}{9} $$
Calculating that gives: $$ -\frac{2 \times 5}{3 \times 9} = -\frac{10}{27} $$
- Apply the law of exponents Next, we'll combine the powers of $h$. We have $h^{3} \times h^{-5}$. According to the law of exponents: $$ h^{a} \times h^{b} = h^{a+b} $$
So: $$ h^{3} \times h^{-5} = h^{3 + (-5)} = h^{-2} $$
-
Combine the results Now, we combine the results from the first two steps: $$ -\frac{10}{27} h^{-2} $$
-
Express with positive exponent (if needed) If you prefer to express the negative exponent positively, we can write: $$ -\frac{10}{27} h^{-2} = -\frac{10}{27} \frac{1}{h^{2}} = -\frac{10}{27h^{2}} $$
The final simplified answer is: $$ -\frac{10}{27h^{2}} $$
More Information
The expression shows how to multiply fractions and apply exponent rules. This type of simplification is common in algebra, especially when dealing with polynomial expressions.
Tips
- Forgetting to add the exponents correctly when multiplying terms with the same base.
- Confusing negative exponents with negative coefficients. Recall that $h^{-n} = \frac{1}{h^{n}}$.
AI-generated content may contain errors. Please verify critical information