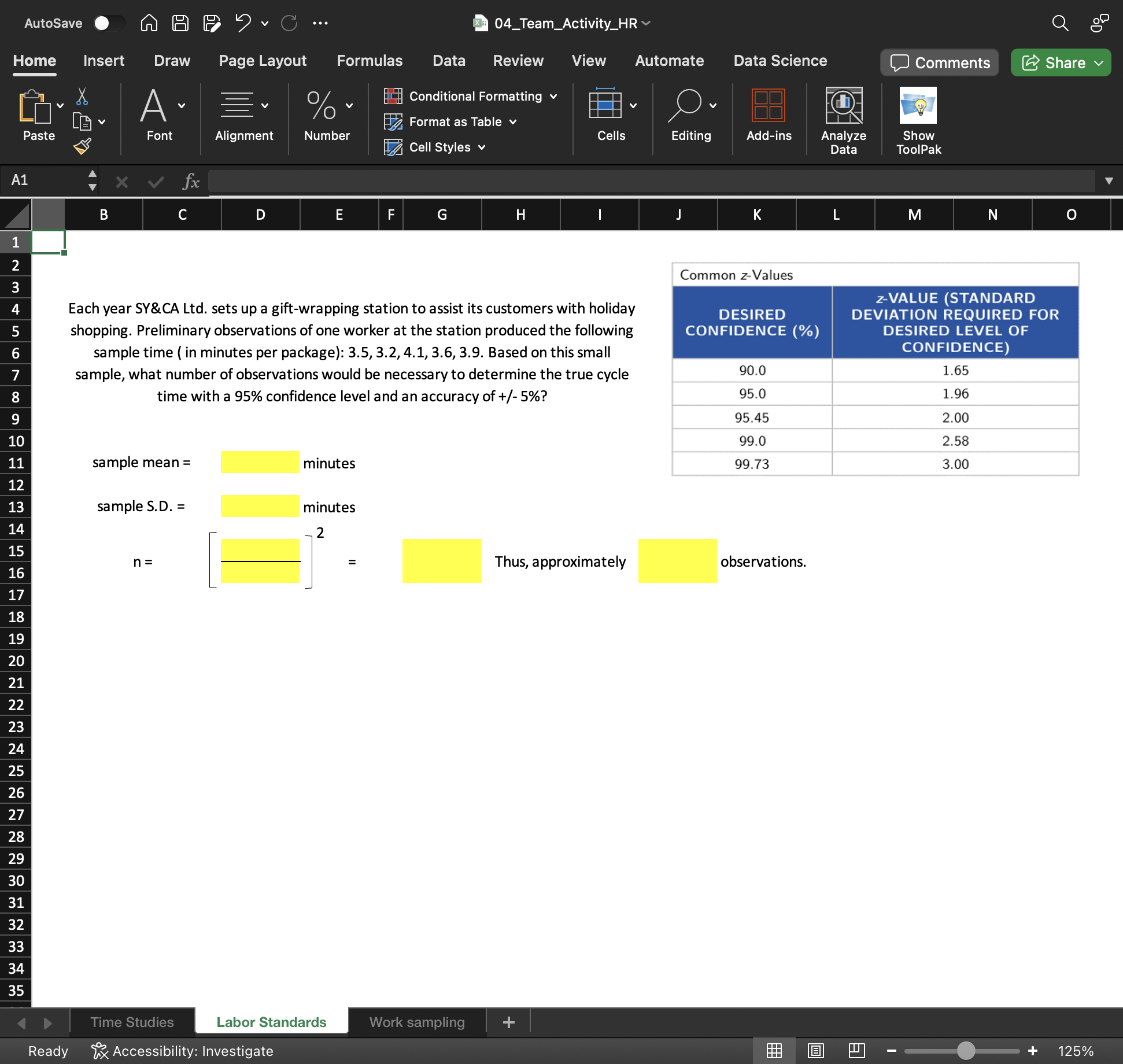
Based on the small sample provided, what number of observations would be necessary to determine the true cycle time with a 95% confidence level and an accuracy of +/- 5%?
Understand the Problem
The question asks for the number of observations needed to determine the true cycle time with a specified confidence level and accuracy. It is based on sample data provided.
Answer
Thus, approximately $n = \left(\frac{1.96 \cdot S.D.}{0.05 \cdot \text{Sample Mean}}\right)^2$ observations.
Answer for screen readers
Thus, approximately ( n = \left(\frac{1.96 \cdot S.D.}{0.05 \cdot \text{Sample Mean}}\right)^2 ) observations.
Steps to Solve
- Calculate the Sample Mean
To find the sample mean, sum all the sample times and divide by the number of observations.
Sample times are: 3.5, 2.3, 5.2, 4.1, 3.6, 3.9.
[ \text{Sample Mean} = \frac{3.5 + 2.3 + 5.2 + 4.1 + 3.6 + 3.9}{6} ]
- Calculate the Sample Standard Deviation (S.D.)
The sample standard deviation can be calculated using the formula:
[ S.D. = \sqrt{\frac{1}{n-1} \sum (x_i - \bar{x})^2} ]
where ( x_i ) is each value and ( \bar{x} ) is the sample mean. Substitute the values and calculate.
- Determine the z-value for 95% Confidence
From the provided z-table, for a 95% confidence level, the z-value is 1.96.
- Calculate the Required Sample Size (n)
Using the formula for sample size based on the desired accuracy (margin of error) and standard deviation:
[ n = \left(\frac{z \cdot S.D.}{E}\right)^2 ]
Where:
- ( z ) is the z-value
- ( S.D. ) is the sample standard deviation calculated from step 2
- ( E ) is the desired margin of error, which is 5% of the sample mean.
- Substitute Values and Solve for n
Insert the calculated values into the sample size formula to determine ( n ).
Thus, approximately ( n = \left(\frac{1.96 \cdot S.D.}{0.05 \cdot \text{Sample Mean}}\right)^2 ) observations.
More Information
To determine the required number of observations for estimating the true cycle time, we need both the mean and standard deviation of the sample. This approach ensures that we capture the variability and accuracy in our observations, providing reliable estimates within the desired confidence level.
Tips
- Forgetting to square the margin of error in the sample size formula.
- Miscalculating the standard deviation; ensure all steps in the calculation are followed.
- Not using the correct z-value for the specified confidence level.
AI-generated content may contain errors. Please verify critical information