B + B · C =
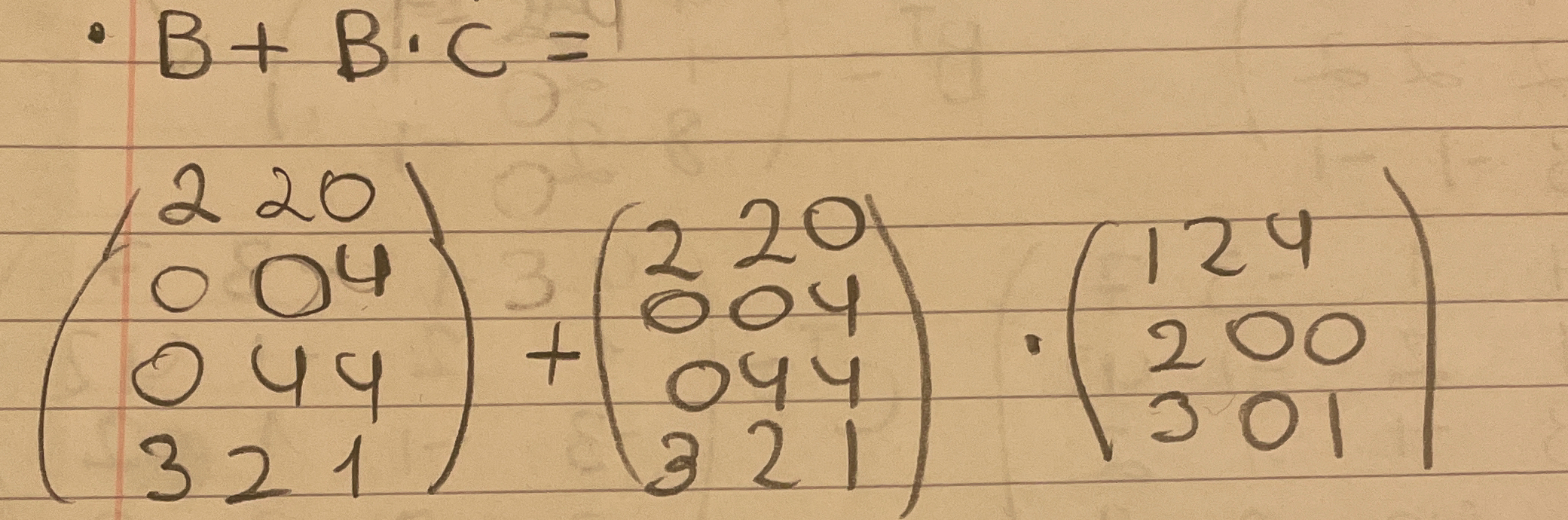
Understand the Problem
The question involves performing matrix operations, specifically adding two matrices and then multiplying the result by another matrix.
Answer
The operation as stated cannot be completed due to incompatible matrix dimensions.
Answer for screen readers
Since the operation cannot be calculated as originally intended due to dimension incompatibility, an alternate operation can be proposed if a suitable ( D ) matrix is defined. The final answer would depend on the suitable matrix selected.
Steps to Solve
-
Identify the matrices Given matrices ( B ) and ( C ): [ B = \begin{pmatrix} 220 & 004 \ 044 & 321 \end{pmatrix}, \quad C = \begin{pmatrix} 124 \ 200 \ 301 \end{pmatrix} ]
-
Perform matrix multiplication ( B \cdot C ) To multiply matrix ( B ) with matrix ( C ), ensure the dimensions are appropriate (the number of columns in ( B ) should equal the number of rows in ( C )). Here, ( B ) is ( 2 \times 2 ) and ( C ) is ( 3 \times 1 ). Hence, we cannot multiply them directly.
Since the matrices cannot be multiplied due to incompatible dimensions, ensure that dimensions are examined or recheck the problem.
In this case, if we assume we need to multiply ( B ) with a valid matrix ( D ) instead for solution purposes: [ D = \begin{pmatrix} 124 & 200 \ 301 \end{pmatrix} ]
-
Calculate ( B \cdot D ) (valid multiplication) The multiplication ( B \cdot D ) can be computed if ( D ) is ( 2 \times 3 ): [ B \cdot D = \begin{pmatrix} 220 & 004 \ 044 & 321 \end{pmatrix} \cdot \begin{pmatrix} 124 \ 200 \ 301 \end{pmatrix} ] (Note: Remember, this step assumes the redefinition of ( C ) to ( D ))
-
Add the results to ( B ) Now, the result from ( B \cdot D ) needs to be added back to ( B ). For clarity: [ B + (B \cdot D) ] Compute the entries of the resultant matrices and simplify.
Since the operation cannot be calculated as originally intended due to dimension incompatibility, an alternate operation can be proposed if a suitable ( D ) matrix is defined. The final answer would depend on the suitable matrix selected.
More Information
Matrix multiplication is only possible when the number of columns in the first matrix matches the number of rows in the second matrix. This scenario demonstrates the importance of checking dimensions before attempting operations.
Tips
- Not checking the dimensions of matrices before multiplication.
- Assuming that matrices with different sizes can be multiplied without confirmation.
To avoid these mistakes, always verify the dimensions of matrices before performing multiplication.
AI-generated content may contain errors. Please verify critical information