Attempt any four of the following: a) Prove that the function f(z) = |z|^2 is not analytic. b) Prove that: |cosh z|^2 = sinh^2 x + cos^2 y c) Find the point at which the functio... Attempt any four of the following: a) Prove that the function f(z) = |z|^2 is not analytic. b) Prove that: |cosh z|^2 = sinh^2 x + cos^2 y c) Find the point at which the function f(z) = xy^2 is analytic. d) Express z = (1 - 2i) in polar form. e) Prove that the two power series Σ an z^n and Σ n an' z^n have the same radius of convergence. f) Find the absolute value and conjugate of z = (2 + i)(4 + 3i).
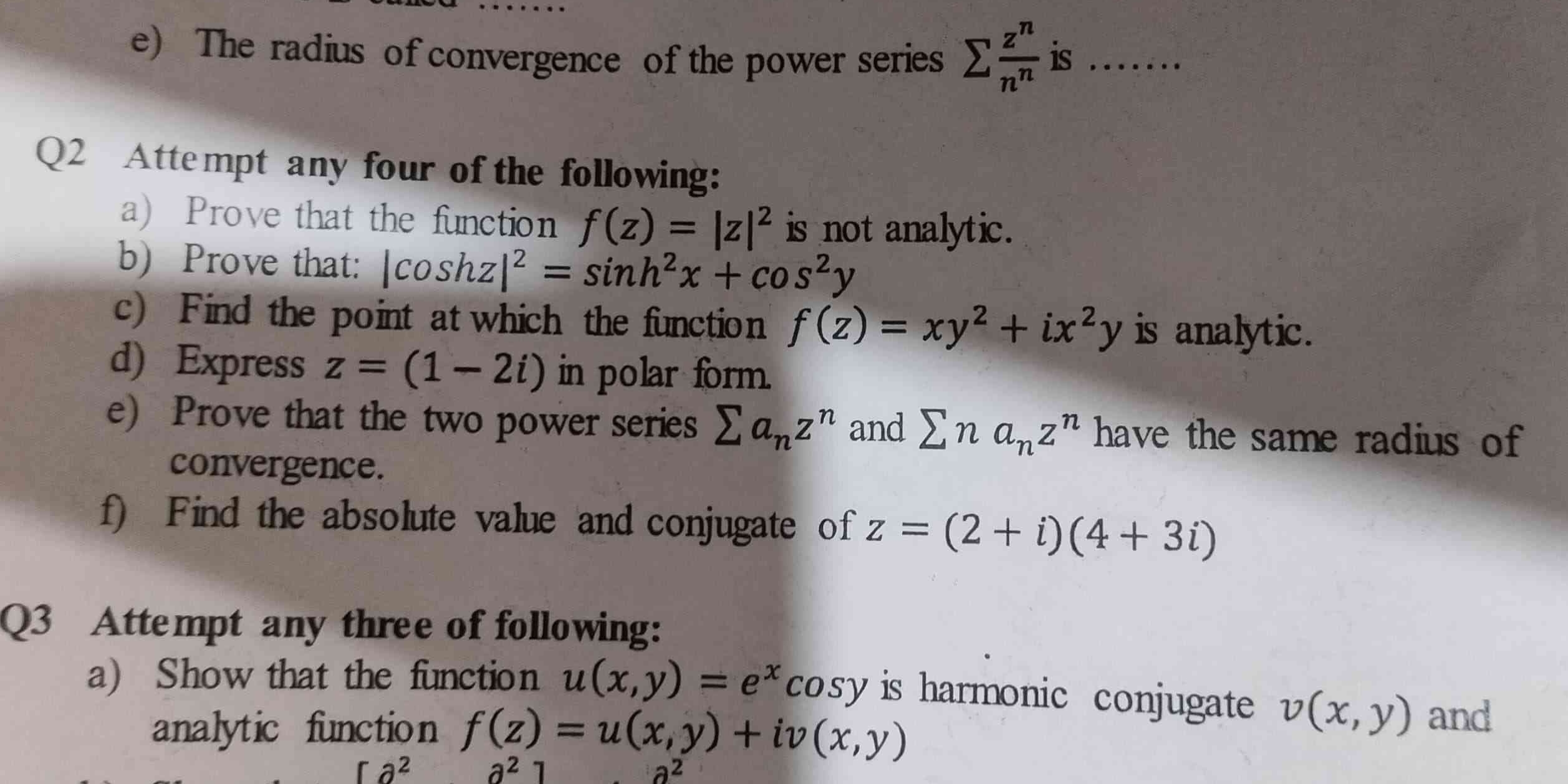
Understand the Problem
The question consists of multiple parts that require proving mathematical concepts related to analytic functions, polar coordinates, power series, and properties of functions in complex analysis. It asks for explorations and proofs about specific functions and convergence criteria.
Answer
1. Not analytic; 2. \( |\cosh z|^2 = \sinh^2 x + \cos^2 y \); 3. \( y = 0 \); 4. \( z = \sqrt{5} (\cos(\theta) + i \sin(\theta)) \) where \( \theta = \tan^{-1}(-2) \)
Answer for screen readers
- ( f(z) = |z|^2 ) is not analytic.
- ( |\cosh z|^2 = \sinh^2 x + \cos^2 y ).
- ( f(z) = xy^2 ) is analytic at ( y = 0 ).
- ( z = \sqrt{5} (\cos(\theta) + i \sin(\theta)) ) where ( \theta = \tan^{-1}(-2) ).
Steps to Solve
- Prove that ( f(z) = |z|^2 ) is not analytic
To show that ( f(z) = |z|^2 ) is not analytic, we can check the Cauchy-Riemann equations. Recall that ( |z|^2 = x^2 + y^2 ), where ( z = x + iy ).
The real part ( u(x, y) = x^2 + y^2 ) and the imaginary part ( v(x, y) = 0 ).
The partial derivatives are:
- ( \frac{\partial u}{\partial x} = 2x )
- ( \frac{\partial u}{\partial y} = 2y )
- ( \frac{\partial v}{\partial x} = 0 )
- ( \frac{\partial v}{\partial y} = 0 )
Now checking the Cauchy-Riemann equations:
- ( \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \implies 2x = 0 ) (only true at ( x = 0 ))
- ( \frac{\partial u}{\partial y} = -\frac{\partial v}{\partial x} \implies 2y = 0 ) (only true at ( y = 0 ))
Since the equations do not hold generally, ( f(z) ) is not analytic.
- Prove that ( |\cosh z|^2 = \sinh^2 x + \cos^2 y )
We start with the definition of ( \cosh z ): $$ \cosh z = \cosh(x + iy) = \cosh x \cos y + i \sinh x \sin y $$
Calculating ( |\cosh z|^2 ): $$ |\cosh z|^2 = (\cosh x \cos y)^2 + (\sinh x \sin y)^2 $$
Expanding: $$ |\cosh z|^2 = \cosh^2 x \cos^2 y + \sinh^2 x \sin^2 y $$
Using the trigonometric identity ( \cos^2 y + \sin^2 y = 1 ): $$ |\cosh z|^2 = \sinh^2 x + (\cosh^2 x - \sinh^2 x) \cos^2 y = \sinh^2 x + \cos^2 y $$
- Find the point where ( f(z) = xy^2 ) is analytic
To find where ( f(z) = xy^2 ) is analytic, identify the real and imaginary parts:
Let ( u(x,y) = xy^2 ) and ( v(x,y) = 0 ).
Compute the partial derivatives:
- ( \frac{\partial u}{\partial x} = y^2 )
- ( \frac{\partial u}{\partial y} = 2xy )
- ( \frac{\partial v}{\partial x} = 0 )
- ( \frac{\partial v}{\partial y} = 0 )
Now check the Cauchy-Riemann equations:
- ( y^2 = 0 ) (implying ( y = 0 ))
- ( 2xy = 0 ) (hold true if ( x = 0 ) or ( y = 0 ))
Thus, ( f(z) ) is analytic at points where ( y = 0 ) (on the real axis).
- Express ( z = (1 - 2i) ) in polar form
To express ( z ) in polar form:
- Find ( r = |z| = \sqrt{(1)^2 + (-2)^2} = \sqrt{1 + 4} = \sqrt{5} )
- Find the angle ( \theta = \tan^{-1}\left(\frac{-2}{1}\right) = \tan^{-1}(-2) )
Thus, in polar form, ( z = \sqrt{5} (\cos \theta + i \sin \theta) ).
- ( f(z) = |z|^2 ) is not analytic.
- ( |\cosh z|^2 = \sinh^2 x + \cos^2 y ).
- ( f(z) = xy^2 ) is analytic at ( y = 0 ).
- ( z = \sqrt{5} (\cos(\theta) + i \sin(\theta)) ) where ( \theta = \tan^{-1}(-2) ).
More Information
The results show significant concepts in complex analysis regarding analyticity, the use of polar coordinates, harmonic functions, and properties of hyperbolic functions.
Tips
- Mixing real and imaginary parts: Always ensure you treat them distinctly and apply the Cauchy-Riemann equations appropriately.
- Confusion in polar forms: Incorrectly determining the angle when converting from Cartesian to polar can lead to errors.
AI-generated content may contain errors. Please verify critical information