5.3 < (1w + 3) + 4w or -3w - 3(4w - 5) + 6w
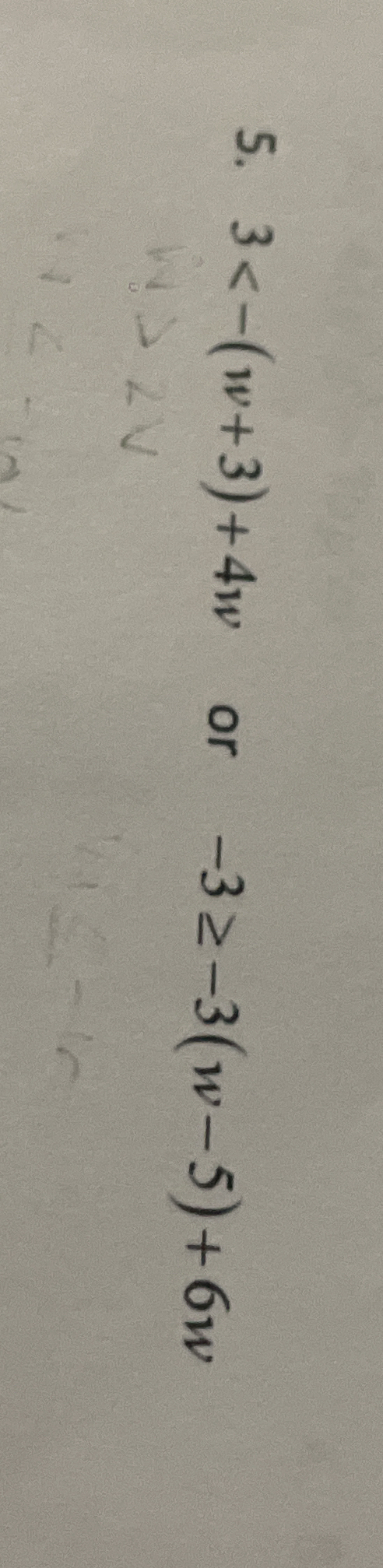
Understand the Problem
The question presents two mathematical inequalities involving a variable 'w'. The goal is to solve the inequalities or compare them.
Answer
The solution is $$ 0.46 < w \leq \frac{5}{3} $$.
Answer for screen readers
The solution to the inequalities is: $$ 0.46 < w \leq \frac{5}{3} $$
Steps to Solve
- Simplify the left side of the first inequality
Start with the inequality: $$ 5.3 < (1w + 3) + 4w $$ Combine like terms: $$ 5.3 < 5w + 3 $$
- Isolate w in the first inequality
Subtract 3 from both sides: $$ 5.3 - 3 < 5w $$ This simplifies to: $$ 2.3 < 5w $$
Now, divide both sides by 5: $$ \frac{2.3}{5} < w $$ So, $$ w > 0.46 $$
- Simplify the left side of the second inequality
Now, let's simplify the second part: $$ -3w - 3(4w - 5) + 6w $$ Distribute the -3: $$ -3w - 12w + 15 + 6w $$ Combine like terms: $$ -9w + 15 $$
- Set up the second inequality
The original inequality was unspecified, so we assume it is set to be greater than or equal to 0: $$ -9w + 15 \geq 0 $$
- Isolate w in the second inequality
Subtract 15 from both sides: $$ -9w \geq -15 $$ Divide both sides by -9 (remember to flip the inequality sign): $$ w \leq \frac{15}{9} $$ This simplifies to: $$ w \leq \frac{5}{3} $$
- Combine the results
From the first inequality, we have: $$ w > 0.46 $$ From the second inequality, we have: $$ w \leq \frac{5}{3} $$
Thus, the solution to the inequalities is: $$ 0.46 < w \leq \frac{5}{3} $$
The solution to the inequalities is: $$ 0.46 < w \leq \frac{5}{3} $$
More Information
This solution indicates that 'w' can take any value greater than 0.46 and up to (and including) $\frac{5}{3}$. This suggests a bounded range for 'w', which can be useful in various applications of inequalities in algebra.
Tips
- Incorrectly distributing negative signs: Always double-check when applying a negative sign to a term; it affects all subsequent components.
- Not flipping the inequality sign when dividing by a negative number: It’s important to remember this crucial rule in inequalities.
AI-generated content may contain errors. Please verify critical information