As per de Broglie wave-particle duality, a plot of wavelength (λ) vs momentum (p) is correct.
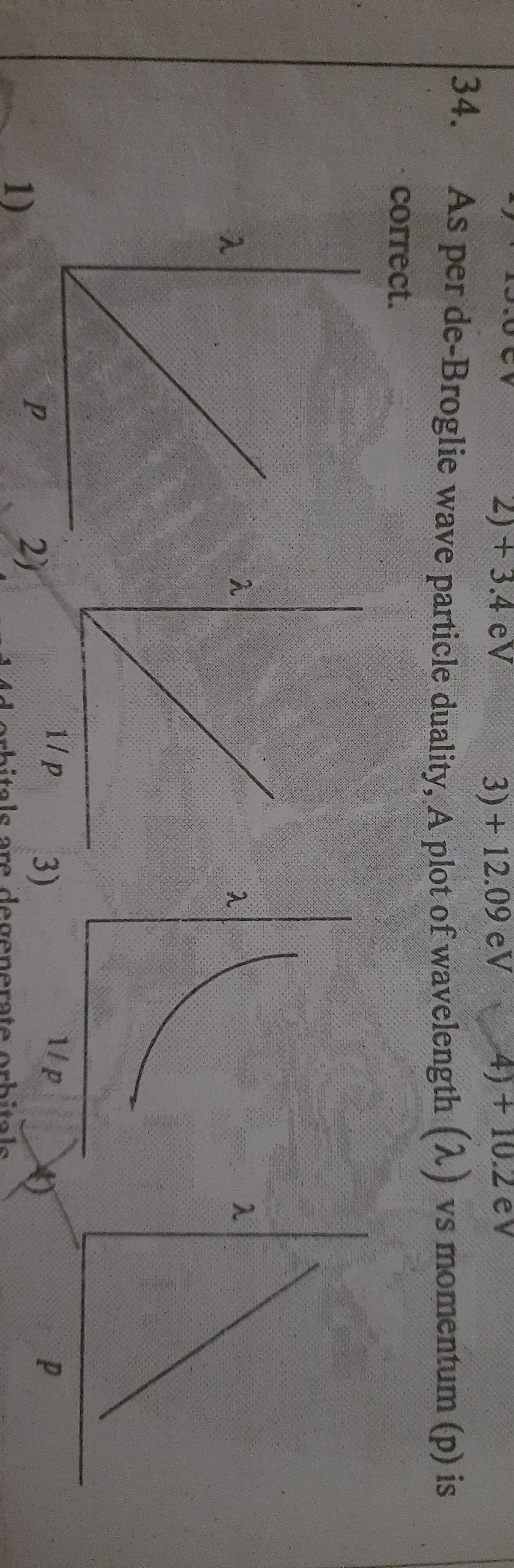
Understand the Problem
The question is requesting to identify the correct plot representing the relation between wavelength and momentum as per de Broglie's wave-particle duality theory.
Answer
The correct plot shows a hyperbolic decline in momentum ($p$) as wavelength ($\lambda$) increases.
Answer for screen readers
The correct plot representing the relation between wavelength ($\lambda$) and momentum ($p$) according to de Broglie's wave-particle duality is the plot that shows a hyperbolic decline.
Steps to Solve
- Understanding de Broglie's Equation
The de Broglie wavelength ($\lambda$) is related to momentum ($p$) by the equation:
$$ \lambda = \frac{h}{p} $$
where $h$ is Planck's constant.
- Rearranging the Equation
From the above relation, we can rearrange to express momentum:
$$ p = \frac{h}{\lambda} $$
This shows that momentum is inversely proportional to wavelength.
- Analyzing the Relationship
As $\lambda$ increases, $p$ decreases. This relationship indicates a hyperbolic decay curve. Therefore, the plot of $p$ versus $\lambda$ will show a downward trend, or more specifically, a hyperbolic shape.
- Selecting the Correct Plot
Out of the given options, the plot that resembles a hyperbolic decline indicates the correct relationship between wavelength and momentum according to de Broglie’s theory.
The correct plot representing the relation between wavelength ($\lambda$) and momentum ($p$) according to de Broglie's wave-particle duality is the plot that shows a hyperbolic decline.
More Information
This relationship illustrates the wave-particle duality of matter, emphasizing how larger wavelengths correspond to lower momentum, a core concept in quantum mechanics.
Tips
- Confusing the direct proportionality with inverse proportionality. Students may mistakenly think that as wavelength increases, momentum increases as well.
- Misinterpreting the graph types and not recognizing the characteristics of hyperbolic relationships.
AI-generated content may contain errors. Please verify critical information