Apply topological sort using DFS?

Understand the Problem

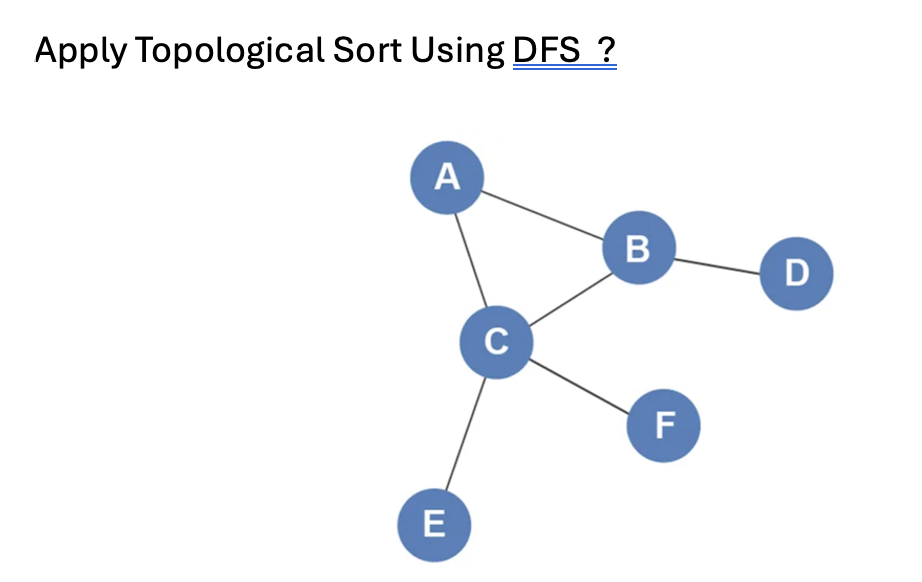
The question is asking for the implementation of a topological sort on a directed graph using Depth-First Search (DFS). This involves traversing the graph while respecting its structure to determine a linear ordering of its vertices.

Answer

The topological order is $A, C, E, F, B, D$.

Steps to Solve

Initialize Data Structures

Start by creating a stack to hold the topological order and a visited set to track the visited nodes.
Define the DFS Function

Create a recursive function that accepts a node, marks it as visited, and visits all its adjacent nodes recursively. After visiting all adjacent nodes, push the node onto the stack.
Perform DFS on All Nodes

Iterate over all nodes in the graph. For each unvisited node, call the DFS function. This ensures that all connected components are covered.
Extract Topological Order

Once all nodes have been processed, the stack will contain the elements in reverse topological order. Pop the elements from the stack to retrieve the correct order.
Return or Output the Topological Order

Return the ordered elements from the stack as the result of the topological sort.

The topological order for the provided directed graph using DFS is: $A, C, E, F, B, D$.

More Information

Topological sorting is useful in scenarios such as scheduling tasks where certain tasks must be completed before others. The directed graph in the image represents dependencies among tasks, and the topological order provides a valid sequence to execute them.

Tips

Forgetting to mark nodes as visited can lead to infinite loops or missing nodes in the topological order.
Not handling disconnected components in the graph properly, which can cause some nodes to be unvisited.
Incorrectly assuming that the order in which nodes are processed reflects the topological sort without considering dependencies.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!