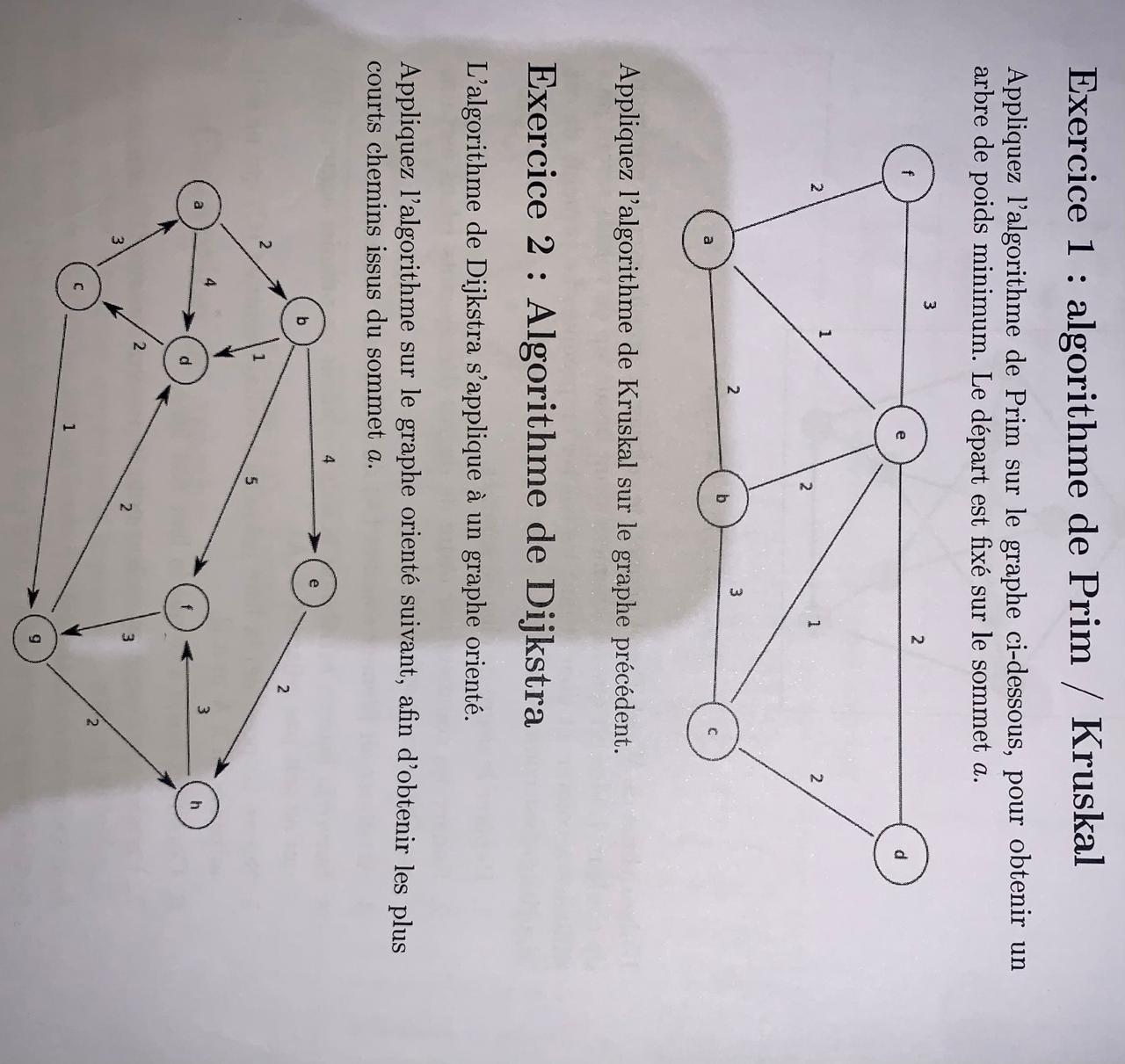
Appliquez l'algorithme de Prim sur le graphe ci-dessus pour obtenir un arbre de poids minimum. Appliquez l'algorithme de Kruskal sur le graphe précédent. Appliquez l'algorithme de... Appliquez l'algorithme de Prim sur le graphe ci-dessus pour obtenir un arbre de poids minimum. Appliquez l'algorithme de Kruskal sur le graphe précédent. Appliquez l'algorithme de Dijkstra sur un graphe orienté suivant afin d'obtenir les plus courts chemins issus du sommet c.
Understand the Problem
La question demande d'appliquer les algorithmes de Prim et de Kruskal sur un graphe donné pour obtenir un arbre de poids minimum. Ensuite, il faut également appliquer l'algorithme de Dijkstra sur un autre graphe orienté pour déterminer les plus courts chemins à partir d'un sommet donné.
Answer
L'arbre de poids minimum a un poids total de $8$, et les plus courts chemins depuis le sommet $c$ sont $d(c) = 0$, $d(e) = 1$, $d(b) = 2$.
Answer for screen readers
L'arbre de poids minimum de l'algorithme de Kruskal est constitué des arêtes $(b, d)$, $(a, b)$, $(b, c)$, $(c, d)$, $(b, e)$ avec un poids total de $8$. Les distances les plus courtes depuis le sommet $c$ dans le graphe orienté sont $d(c) = 0$ (c), $d(e) = 1$, et $d(b) = 2$.
Steps to Solve
- Application de l'algorithme de Kruskal
Commencez par nommer tous les sommets du graphe, puis triez les arêtes par poids.
Les arêtes sont:
- $(a, b, 2)$
- $(b, c, 2)$
- $(c, d, 2)$
- $(b, e, 3)$
- $(a, e, 3)$
- $(d, e, 4)$
- $(a, c, 4)$
- $(b, d, 1)$
- $(e, f, 3)$
Ajoutez les arêtes en évitant les cycles jusqu'à obtenir un arbre couvrant.
- Construction de l'arbre avec Kruskal
Ajoutez progressivement les arêtes en vérifiant qu'elles ne forment pas de cycles:
- Ajoutez $(b, d)$
- Ajoutez $(a, b)$
- Ajoutez $(b, c)$
- Ajoutez $(c, d)$
- Ajoutez $(b, e)$
Résultat final de l'arbre de poids minimum: $(a-b-c-d-e)$ avec un poids total de $2+2+1+3=8$.
- Application de l'algorithme de Dijkstra
Pour déterminer les plus courts chemins depuis le sommet $c$ sur le graphe orienté, commencez par initialiser les distances et le sommet de départ:
- Distance initiale: $d(c) = 0$ et pour tous les autres $d(x) = \infty$.
- Mise à jour des distances
Pour chaque sommet, calculez la distance en parcourant les arêtes sorties de $c$ et mettez à jour les distances. Répétez jusqu'à ce que toutes les distances soient connues:
- Pour $c$: $d(c) = 0$.
- Pour les voisins $e$ et $b$: $d(e) = 1$ (de $c$) et $d(b) = 2$ (de $c$).
Continuez jusqu'à explorer tous les sommets.
L'arbre de poids minimum de l'algorithme de Kruskal est constitué des arêtes $(b, d)$, $(a, b)$, $(b, c)$, $(c, d)$, $(b, e)$ avec un poids total de $8$. Les distances les plus courtes depuis le sommet $c$ dans le graphe orienté sont $d(c) = 0$ (c), $d(e) = 1$, et $d(b) = 2$.
More Information
L'algorithme de Kruskal est utilisé pour trouver un arbre couvrant minimal en triant les arêtes par poids et en les ajoutant sans former de cycles. L'algorithme de Dijkstra, quant à lui, est utilisé pour trouver les plus courts chemins à partir d'un sommet donné dans un graphe orienté.
Tips
- Ne pas trier correctement les arêtes dans l'algorithme de Kruskal.
- Oublier de vérifier les cycles lors de l'ajout des arêtes.
- Ne pas mettre à jour correctement les distances dans l'algorithme de Dijkstra, en négligeant certains sommets ou en utilisant de mauvaises valeurs de distance.
AI-generated content may contain errors. Please verify critical information