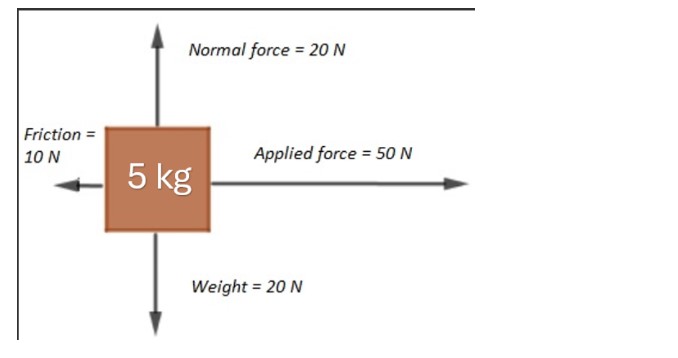
Analyze the forces acting on a 5 kg object with a normal force of 20 N, friction of 10 N, and an applied force of 50 N.
Understand the Problem
The question appears to be related to the forces acting on a 5 kg object, including normal force, friction, applied force, and weight. We need to analyze these forces, likely to understand the net force or to solve for acceleration using Newton's second law.
Answer
The acceleration of the object is $8 \, \text{m/s}^2$.
Answer for screen readers
The acceleration of the object is $8 , \text{m/s}^2$.
Steps to Solve
- Identify the forces acting on the object
The object has four main forces acting on it:
- Normal Force ($F_N = 20 , \text{N}$) acting upward
- Weight ($W = 20 , \text{N}$) acting downward
- Applied Force ($F_a = 50 , \text{N}$) acting horizontally to the right
- Friction Force ($F_f = 10 , \text{N}$) acting horizontally to the left
- Calculate the net vertical force
The net vertical force is the difference between the normal and weight forces:
$$ F_{\text{net, vertical}} = F_N - W = 20 , \text{N} - 20 , \text{N} = 0 , \text{N} $$
- Calculate the net horizontal force
The net horizontal force is calculated by subtracting the frictional force from the applied force:
$$ F_{\text{net, horizontal}} = F_a - F_f = 50 , \text{N} - 10 , \text{N} = 40 , \text{N} $$
- Apply Newton's second law
Using Newton's second law, we can find the acceleration of the object:
$$ F_{\text{net}} = m \cdot a $$
Substituting the net horizontal force and mass:
$$ 40 , \text{N} = 5 , \text{kg} \cdot a $$
- Solve for acceleration
To find the acceleration, rearrange the equation:
$$ a = \frac{F_{\text{net}}}{m} = \frac{40 , \text{N}}{5 , \text{kg}} = 8 , \text{m/s}^2 $$
The acceleration of the object is $8 , \text{m/s}^2$.
More Information
This result indicates that the object will accelerate to the right at $8 , \text{m/s}^2$ due to the net horizontal force acting on it. The balance of vertical forces shows that it is not accelerating vertically; thus, it remains on the surface.
Tips
- Forgetting to consider both the normal force and the weight when calculating vertical forces.
- Neglecting to properly subtract friction from the applied force in horizontal force calculations.
- Misapplying Newton's second law, particularly forgetting the mass when calculating acceleration.
AI-generated content may contain errors. Please verify critical information