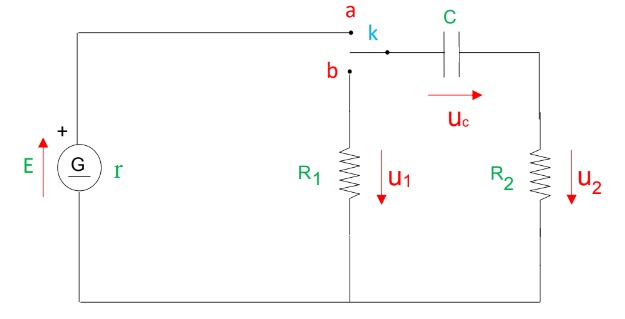
Analyze the circuit and determine the voltages U1, U2, and Uc.
Understand the Problem
The question appears to relate to an electrical circuit involving resistors and a capacitor. It likely pertains to the analysis of the voltage across different components in the circuit. To solve it, we would need to apply Kirchhoff's laws or the principles of circuit analysis.
Answer
The voltage across the capacitor is described by: $$ \frac{dU_c}{dt} + \frac{(R_1 + R_2)}{C} U_c = E $$
Answer for screen readers
The equation describing the voltage across the capacitor over time is: $$ \frac{dU_c}{dt} + \frac{(R_1 + R_2)}{C} U_c = E $$
Steps to Solve
-
Identify the circuit components This circuit contains a voltage source ($E$), a resistance ($r$), two resistors ($R_1$ and $R_2$), and a capacitor ($C$).
-
Apply Kirchhoff's Voltage Law (KVL) According to KVL, the sum of the voltage drops across the components must equal the supplied voltage. The equation can be set up: $$ E - U_1 - U_c - U_2 = 0 $$
-
Define Voltage Across Resistors The voltage across each resistor can be described using Ohm's Law:
- For $R_1$: $$ U_1 = I \cdot R_1 $$
- For $R_2$: $$ U_2 = I \cdot R_2 $$
-
Express Current through the Capacitor The current ($I$) through the capacitor can be expressed as: $$ I = \frac{dQ}{dt} = C \frac{dU_c}{dt} $$ where $Q$ is the charge on the capacitor.
-
Substitute in KVL Equation Replace $U_1$ and $U_2$ in the KVL equation with their expressions from Ohm's Law: $$ E - I \cdot R_1 - U_c - I \cdot R_2 = 0 $$ Combine terms: $$ E - I(R_1 + R_2) - U_c = 0 $$
-
Solve for Voltage Across the Capacitor Rearranging gives: $$ U_c = E - I(R_1 + R_2) $$
-
Substituting Current Expression Substituting the expression for $I$: $$ U_c = E - C\frac{dU_c}{dt}(R_1 + R_2) $$
-
Formulating a Differential Equation This leads to a differential equation that can be solved for $U_c$ over time: $$ \frac{dU_c}{dt} + \frac{(R_1 + R_2)}{C} U_c = E $$
The equation describing the voltage across the capacitor over time is: $$ \frac{dU_c}{dt} + \frac{(R_1 + R_2)}{C} U_c = E $$
More Information
This differential equation represents the behavior of the voltage across a capacitor in an RC circuit. The solution provides insight into how the voltage builds up over time after the circuit is energized.
Tips
- Forgetting to account for the voltage across the capacitor when applying KVL.
- Not correctly applying Ohm's Law for resistors in series or parallel correctly.
- Confusing current through the capacitor with the steady-state current when solving.
AI-generated content may contain errors. Please verify critical information