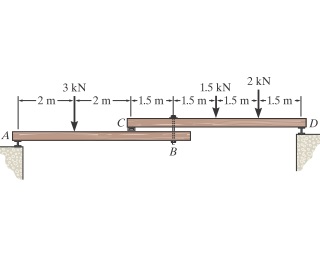
Analyze the beam system with the given loads and distances, and calculate the reactions at supports A and D.

Understand the Problem

The question involves analyzing a structural support system with multiple forces acting on beams at points A, B, C, and D. The key is to determine how these forces affect the system and to possibly calculate reactions or moments.

Answer

The reactions are $R_A = 1.875 \, kN$ and $R_D = 4.625 \, kN$.

Steps to Solve

Identify the Forces and Moments List all the forces acting on the beams. In this case, the forces are:

$F_A = 3 , kN$ at point A
$F_C = 1.5 , kN$ at point C
$F_D = 2 , kN$ at point D
The weight of the beams can also be considered if they are significant.

Calculate Reactions at Supports A and D Using the static equilibrium conditions, we can calculate the reactions. For vertical forces, the sum should equal zero: $$ R_A + R_D - F_A - F_C - F_D = 0 $$
Apply Moment Equations Choose point A to sum moments. The moment due to a force is calculated as: $$ \text{Moment} = \text{Force} \times \text{Distance} $$ Set the sum of moments about point A equal to zero: $$ R_D \times 6 - 3 \times 2 - 1.5 \times 4.5 - 2 \times 7.5 = 0 $$
Calculating the Reactions Solve the moment equation for $R_D$: $$ R_D = \frac{3 \times 2 + 1.5 \times 4.5 + 2 \times 7.5}{6} $$

Once you find $R_D$, substitute back into the vertical force equilibrium equation to find $R_A$.

Final Calculation for Forces After finding the values of $R_A$ and $R_D$, ensure they satisfy both equilibrium equations, confirming that all forces and moments balance.

Let’s solve for the reactions.

Calculate $R_D$: $$ R_D = \frac{3 \times 2 + 1.5 \times 4.5 + 2 \times 7.5}{6} = \frac{6 + 6.75 + 15}{6} = \frac{27.75}{6} = 4.625 , kN $$
Substituting back to find $R_A$: $$ R_A = F_A + F_C + F_D - R_D = 3 + 1.5 + 2 - 4.625 = 1.875 , kN $$

Thus, the reactions are:

$R_A = 1.875 , kN$
$R_D = 4.625 , kN$

More Information

The calculations of reactions at the supports are crucial for understanding how the forces distributed throughout the structure impact its stability. In real-world applications, this analysis is vital in engineering, especially for ensuring that structures can withstand loads without failing.

Tips

Forgetting to consider all forces: Always check that all external loads are accounted for.
Misplacing distances when calculating moments: Ensure that distances are measured correctly according to the chosen point for moment calculations.
Not checking if the equilibrium conditions are satisfied: Double-check all calculations to confirm that both sum of vertical forces and sum of moments balance.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!