Understand the Problem
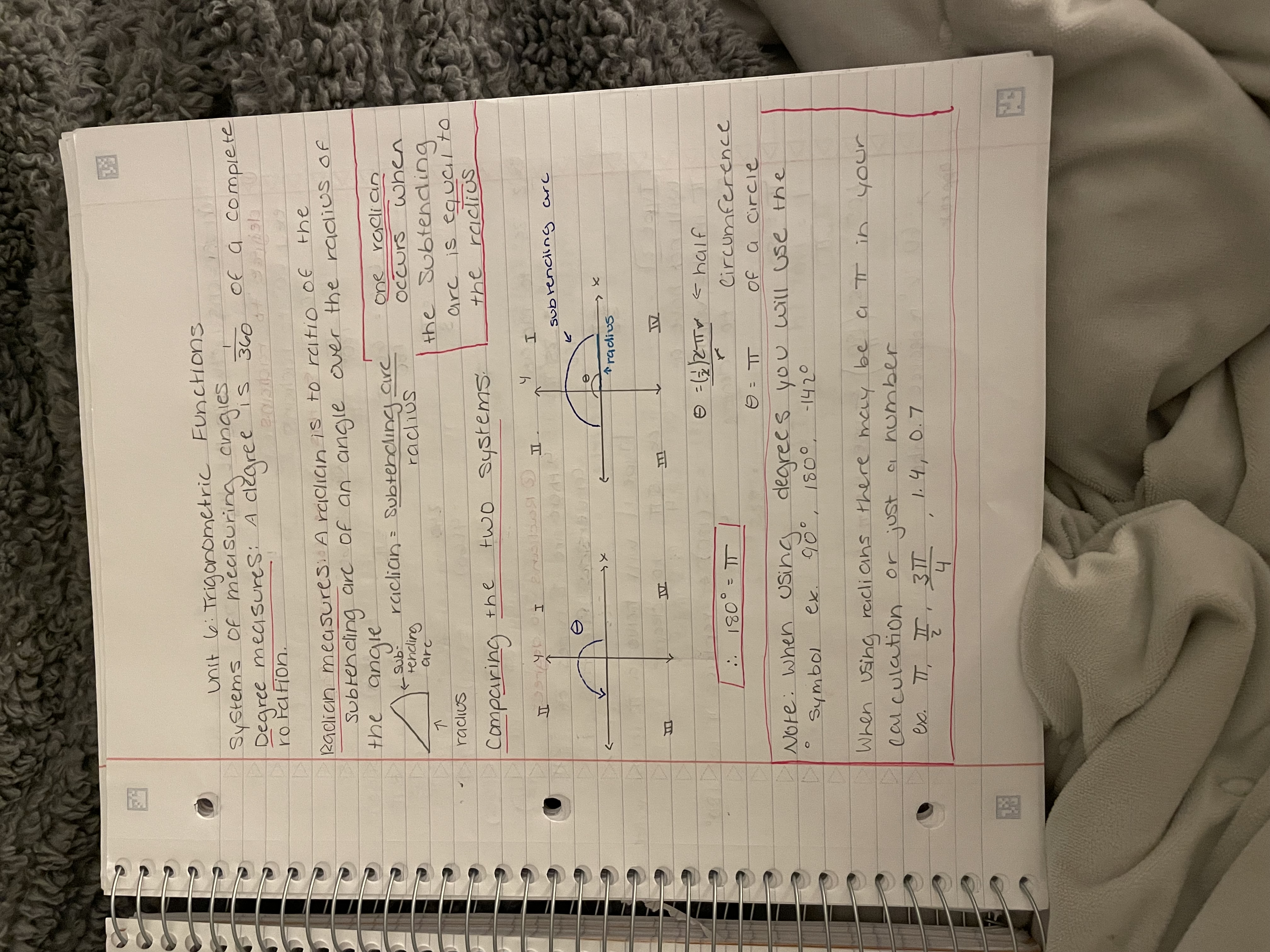
The content discusses the systems of measuring angles in degrees and radians, explaining their definitions and relationships, specifically focusing on how one radian is defined and the conversions between degrees and radians.
Answer
Degrees are 1/360 of a circle; radians are based on arc/radius. 180° = π radians.
The key difference is that degrees measure angles as parts of a full circle (1/360), while radians measure angles based on the radius and arc length. 180° equals π radians.
Answer for screen readers
The key difference is that degrees measure angles as parts of a full circle (1/360), while radians measure angles based on the radius and arc length. 180° equals π radians.
More Information
Radians offer a natural way of measuring angles in terms of the radius and arc length, often useful in calculus and trigonometry.
Tips
A common mistake is mixing degrees and radians in calculations without converting one to the other.
AI-generated content may contain errors. Please verify critical information