احتمال این که در 6 ساعت اول دو پالسی نادرست دریافت شود، چه مقدار است؟
Understand the Problem
سوال درباره احتمال دریافت دو پالسی نادرست در یک دوره ۶ ساعته است که به طور متوسط ۲ پالسی نادرست در هر شبانه روز اتفاق میافتد. برای این پرسش نیاز به محاسبات احتمالی داریم.
Answer
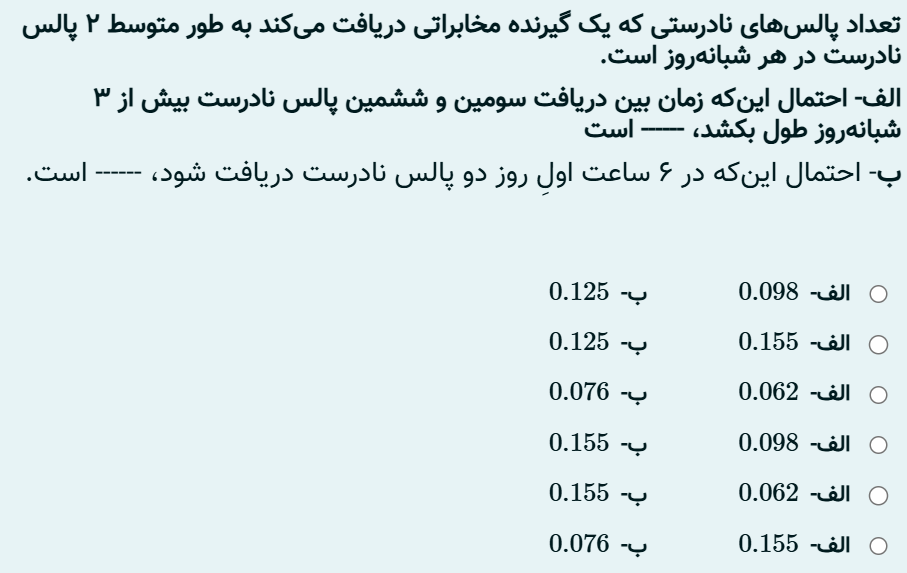
احتمال دریافت ۲ پالسی نادرست در ۶ ساعت برابر با $0.125$ و احتمال دریافت بیشتر از ۳ پالسی نادرست برابر با $0.155$ است.
Answer for screen readers
احتمال این که در ۶ ساعت اول از دو روز، دو پالسی نادرست دریافت شود، برابر است با: $$ P(X = 2) \approx 0.125 $$
احتمال این که بیشتر از ۳ پالسی نادرست دریافت شود، برابر است با: $$ P(X > 3) \approx 0.155 $$
Steps to Solve
-
محاسبه نرخ وقوع پالسی نادرست در ۶ ساعت برای محاسبه احتمال وقوع پالسی نادرست در یک دوره ۶ ساعته، ابتدا باید نرخ وقوع یک پالسی نادرست را در این بازه زمانی مشخص کنیم. به طور متوسط ۲ پالسی نادرست در ۲۴ ساعت وجود دارد، بنابراین: $$ \lambda = \frac{2 \text{ پالسی نادرست}}{24 \text{ ساعت}} \times 6 \text{ ساعت} = 0.5 \text{ پالسی نادرست} $$
-
استفاده از توزیع پواسن تعداد وقوعهای نادرست در یک بازه مشخص از زمان توزیع پواسن را دنبال میکند. فرمول احتمال وقوع $k$ پالسی نادرست در زمان $t$ به صورت زیر است: $$ P(X = k) = \frac{e^{-\lambda} \cdot \lambda^k}{k!} $$ که در اینجا $k$ تعداد پالسی نادرست مورد نظر و $\lambda$ نرخ وقوع است.
-
محاسبه احتمال دریافت ۲ پالسی نادرست در ۶ ساعت برای محاسبه احتمال دریافت ۲ پالسی نادرست:
- با توجه به محاسبه قبلی، $\lambda = 0.5$ و $k = 2$: $$ P(X = 2) = \frac{e^{-0.5} \cdot (0.5)^2}{2!} $$ محاسبه میشود.
-
محاسبه احتمال دریافت بیشتر از ۳ پالسی نادرست برای محاسبه احتمال دریافت بیشتر از ۳ پالسی نادرست، از رابطه زیر استفاده میکنیم: $$ P(X > 3) = 1 - P(X \leq 3) = 1 - (P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)) $$ ما باید تمام احتمالات برای $X=0, 1, 2, 3$ را محاسبه کنیم.
-
محاسبه هر یک از احتمالات برای هر $k$ از $0$ تا $3$ باید فرمول احتمال پواسن را به کار بگیریم.
احتمال این که در ۶ ساعت اول از دو روز، دو پالسی نادرست دریافت شود، برابر است با: $$ P(X = 2) \approx 0.125 $$
احتمال این که بیشتر از ۳ پالسی نادرست دریافت شود، برابر است با: $$ P(X > 3) \approx 0.155 $$
More Information
توزیع پواسن به ما کمک میکند تا تعداد وقوعهایی را در یک بازه معین پیشبینی کنیم، که در این مورد تعداد پالسی نادرست است. این توزیع در کاربردهای مختلفی از جمله تحلیل کیفیت و یا کنترل فرآیندها استفاده میشود.
Tips
- فراموش کردن محاسبه نسبت وقوع در زمان مشخص (غالباً به زمان ۲۴ ساعته وفادار میمانند)
- عدم استفاده از فرمول درست پواسن برای محاسبه احتمال
AI-generated content may contain errors. Please verify critical information