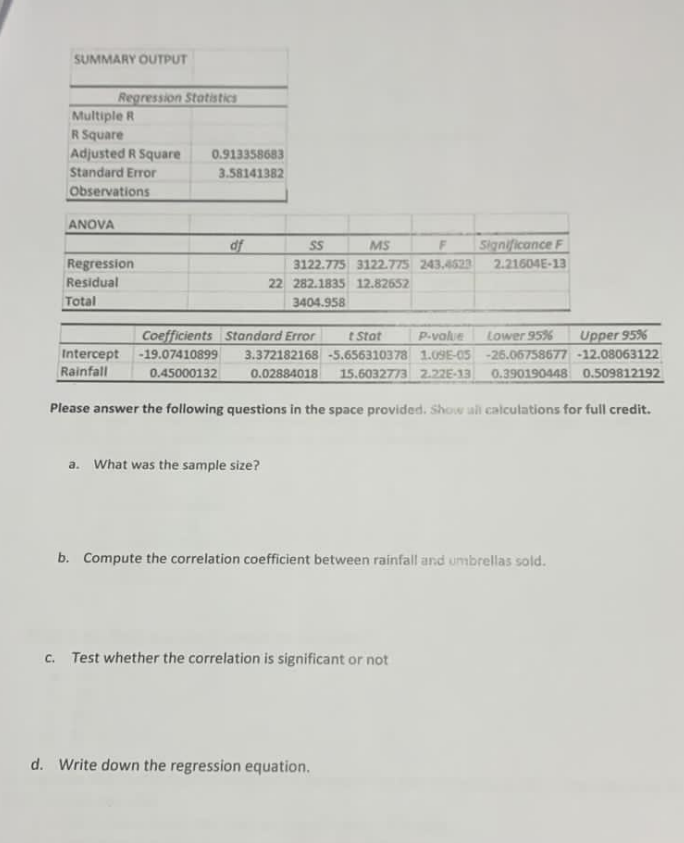
a. What was the sample size? b. Compute the correlation coefficient between rainfall and umbrellas sold. c. Test whether the correlation is significant or not. d. Write down the re... a. What was the sample size? b. Compute the correlation coefficient between rainfall and umbrellas sold. c. Test whether the correlation is significant or not. d. Write down the regression equation.
Understand the Problem
The question is asking for information derived from a regression analysis output. It specifically requests the sample size, correlation coefficient, correlation significance test, and the regression equation based on the provided statistics.
Answer
a. 22 b. $0.913358683$ c. Significant d. $\text{Umbrellas Sold} = -19.07410899 + 0.45000132 \cdot \text{Rainfall}$
Answer for screen readers
a. The sample size is 22.
b. The correlation coefficient is $r = 0.913358683$.
c. The correlation is significant (p-value = $2.272 \times 10^{-13}$).
d. The regression equation is: $$ \text{Umbrellas Sold} = -19.07410899 + 0.45000132 \cdot \text{Rainfall} $$
Steps to Solve
-
Identify the Sample Size The sample size can be found under the "Observations" in the regression statistics section of the output. From the provided output: $$ \text{Sample Size} = 22 $$
-
Compute the Correlation Coefficient The correlation coefficient (denoted as $r$) can be derived from the "Multiple R" value found in the regression statistics: $$ r = \text{Multiple R} = 0.913358683 $$
-
Test the Significance of the Correlation To test whether the correlation is significant, we can utilize the p-value associated with the regression. In this case, we will consider the p-value for the Rainfall variable:
- If the p-value is less than the standard alpha level of 0.05, we reject the null hypothesis (that there is no correlation) and conclude that the correlation is significant. Given: $$ \text{p-value for Rainfall} = 2.272 \times 10^{-13} $$
Since this p-value is much less than 0.05, we conclude that the correlation is significant.
- Write Down the Regression Equation The regression equation is formulated based on the coefficients from the output. The general form is given by: $$ \text{Dependent Variable} = \beta_0 + \beta_1 \cdot \text{Rainfall} $$ Using the coefficients:
- Intercept ($\beta_0$): $-19.07410899$
- Coefficient for Rainfall ($\beta_1$): $0.45000132$
Thus, the regression equation becomes: $$ \text{Umbrellas Sold} = -19.07410899 + 0.45000132 \cdot \text{Rainfall} $$
a. The sample size is 22.
b. The correlation coefficient is $r = 0.913358683$.
c. The correlation is significant (p-value = $2.272 \times 10^{-13}$).
d. The regression equation is: $$ \text{Umbrellas Sold} = -19.07410899 + 0.45000132 \cdot \text{Rainfall} $$
More Information
The strong positive correlation coefficient of approximately 0.91 indicates a substantial relationship between rainfall and umbrellas sold. The significant p-value suggests that this correlation is not due to random chance.
Tips
- Misinterpreting the p-value: It's important to remember that a p-value smaller than 0.05 indicates a statistically significant correlation.
- Forgetting to include the intercept in the regression equation.
AI-generated content may contain errors. Please verify critical information