A sheet described by 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 and z = 0 planes has a charge density ρs (n C/m²). Find (i) the total charge on the sheet, (ii) the electric field at (0,0,5), and (iii) t... A sheet described by 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 and z = 0 planes has a charge density ρs (n C/m²). Find (i) the total charge on the sheet, (ii) the electric field at (0,0,5), and (iii) the electric force by a -1 mC charge located at (0,0,5).
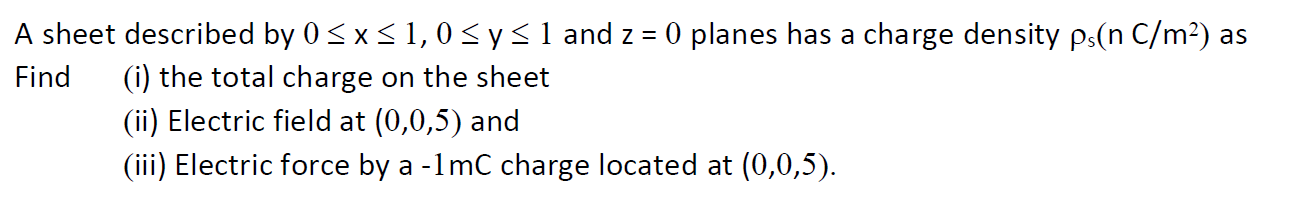
Understand the Problem
The question is asking for three specific calculations based on a charged sheet described in a 3D coordinate system. It requires finding the total charge of the sheet, the electric field at a specific point, and the electric force acting on a given charge due to the electric field.
Answer
1. \( Q = \rho_s \, \text{nC} \) 2. \( E = \frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}} \) 3. \( F = -1 \times 10^{-3} \cdot \left(\frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}}\right) \)
Answer for screen readers
-
Total charge on the sheet: ( Q = \rho_s , \text{nC} )
-
Electric field at (0, 0, 5):
$$ E = \frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}} , \text{N/C} $$
- Electric force on a -1 mC charge:
$$ F = -1 \times 10^{-3} \cdot \left(\frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}}\right) , \text{N} $$
Steps to Solve
- Calculate Total Charge on the Sheet
To find the total charge ( Q ) on the sheet, use the formula:
$$ Q = \sigma \cdot A $$
where ( \sigma ) is the surface charge density ( \rho_s ) (in nC/m²) and ( A ) is the area of the sheet. Given the dimensions ( 0 \leq x \leq 1 ) and ( 0 \leq y \leq 1 ), the area ( A ) is:
$$ A = \Delta x \cdot \Delta y = (1 - 0)(1 - 0) = 1 , \text{m}^2 $$
Thus, the total charge is:
$$ Q = \rho_s \cdot 1 , \text{m}^2 = \rho_s , \text{nC} $$
- Determine the Electric Field at (0, 0, 5)
The electric field ( E ) due to an infinite sheet of charge is given by:
$$ E = \frac{\sigma}{2\epsilon_0} $$
where ( \epsilon_0 ) is the permittivity of free space ( (8.85 \times 10^{-12} , \text{C}^2/\text{N} \cdot \text{m}^2) ).
Substituting ( \sigma ):
$$ E = \frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}} $$
Since the sheet is positively charged, the electric field will point away from the sheet in the positive z-direction.
- Calculate Electric Force on a -1 mC Charge
The electric force ( F ) acting on a charge ( q ) located in an electric field ( E ) is given by:
$$ F = q \cdot E $$
Here, ( q = -1 , \text{mC} = -1 \times 10^{-3} , \text{C} ).
Substituting the value of ( E ) from step 2:
$$ F = (-1 \times 10^{-3}) \cdot \left(\frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}}\right) $$
The direction of the force will be opposite to that of the electric field since the charge is negative.
-
Total charge on the sheet: ( Q = \rho_s , \text{nC} )
-
Electric field at (0, 0, 5):
$$ E = \frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}} , \text{N/C} $$
- Electric force on a -1 mC charge:
$$ F = -1 \times 10^{-3} \cdot \left(\frac{\rho_s \times 10^{-9}}{2 \times 8.85 \times 10^{-12}}\right) , \text{N} $$
More Information
This solution provides a clear breakdown of how to calculate total charge, electric field, and electric force for a charged sheet. Understanding the effect of charge density and area is crucial in electrostatics.
Tips
- Confusing area units: Ensure to use consistent units (e.g., converting nC to C when necessary).
- Misapplying the electric field formula: Remember that the formula for an infinite sheet assumes uniform charge distribution.
- Neglecting the direction of electric field and force for negative charges.
AI-generated content may contain errors. Please verify critical information